Задачи без ограничений. Признаки экстремума
Функция одной переменной. Пусть
необходимо найти экстремум дважды непрерывно
дифференцируемой функции ![]() , где
, где ![]() - вещественная переменная,
- вещественная переменная, ![]() .
.
Определение 1. Точка ![]() называется стационарной для функции
называется стационарной для функции ![]() , если производная функции
в этой точке обращается в нуль,
, если производная функции
в этой точке обращается в нуль, ![]() .
.
Теорема 1. (Необходимый признак). Для того чтобы функция ![]() имела в точке
имела в точке ![]() экстремум, необходимо,
чтобы эта точка была стационарной.
экстремум, необходимо,
чтобы эта точка была стационарной.
Доказательство.
Предположим, что ![]() - точка локального
максимума, тогда для любого, достаточно малого приращения
- точка локального
максимума, тогда для любого, достаточно малого приращения ![]() справедливо неравенство
справедливо неравенство
![]() .
.
Если
![]() , то приращения аргумента и функции имеют разные знаки,
поэтому
, то приращения аргумента и функции имеют разные знаки,
поэтому
![]() .
.
Если
![]() , то приращения аргумента и функции имеют один знак,
поэтому
, то приращения аргумента и функции имеют один знак,
поэтому
![]() .
.
Поскольку
предполагается, что целевая функция непрерывна
в точке ![]() , правый и левый пределы
должны совпадать. Но это в данном случае значит, что
, правый и левый пределы
должны совпадать. Но это в данном случае значит, что
![]() .
.
Аналогичные
рассуждения можно сделать, исходя из предположения, что ![]() - точка локального
минимума.
- точка локального
минимума.
Теорема
доказана.
Теорема 2. (Достаточный признак). Пусть ![]() - стационарная точка
функции
- стационарная точка
функции ![]() . Тогда если
. Тогда если ![]() то
то ![]() - точка локального
максимума; если
- точка локального
максимума; если ![]() то
то ![]() - точка локального
минимума.
- точка локального
минимума.
Доказательство. Разложим
функцию в стационарной точке ![]() в ряд Тейлора:
в ряд Тейлора:
![]() ,
,
где ![]() - бесконечно малая, более высокого порядка
малости, чем
- бесконечно малая, более высокого порядка
малости, чем ![]() .
.
Поскольку
![]() то
то
![]() .
.
Если
![]() то независимо от знака
приращения выполняется соотношение
то независимо от знака
приращения выполняется соотношение ![]() . Но это значит, что
. Но это значит, что ![]() - точка максимума. Аналогично
можно доказать эту теорему для случая
- точка максимума. Аналогично
можно доказать эту теорему для случая ![]() .
.
Теорема
доказана.
Замечание 1.. Если
вторая производная обращается в нуль, то статус стационарной точки остается
неопределенным. Необходимо рассматривать производные более высоких порядков.
Пусть производные всех порядков до ![]() -го оказались равны нулю, а
-го оказались равны нулю, а ![]() . Тогда если
. Тогда если ![]() - четное число и
- четное число и ![]() , то имеем локальный максимум, если
, то имеем локальный максимум, если ![]() , то минимум. Если же
, то минимум. Если же ![]() - нечетное число, то
экстремума нет.
- нечетное число, то
экстремума нет.
Функция
многих переменных. Пусть ![]() - дважды непрерывно дифференцируемая
функция векторного аргумента
- дважды непрерывно дифференцируемая
функция векторного аргумента ![]() , где
, где ![]() .
.
Теорема 3. (Необходимый признак). Для того чтобы функция ![]() имела в точке
имела в точке ![]() экстремум, необходимо,
чтобы все ее частные производные в этой
точке обращались в нуль:
экстремум, необходимо,
чтобы все ее частные производные в этой
точке обращались в нуль:
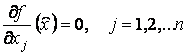
Доказательство.
Зафиксируем все переменные кроме ![]() , положив, что
, положив, что ![]() для всех
для всех ![]() . Рассмотрим функцию
. Рассмотрим функцию ![]() . Если
. Если ![]() - экстремальная точка
функции
- экстремальная точка
функции ![]() , то
, то
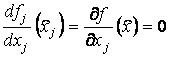 .
.
Распространяя
этот результат на остальные переменные, приходим к выводу о справедливости
утверждения теоремы.
Замечание 2. Из
необходимого условия вполне очевидно следует равенство нулю дифференциала функции ![]() в точке
в точке ![]() :
:
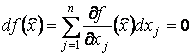 .
.
Справедливо
и обратное утверждение. В силу произвольности ![]() дифференциал функции
равен нулю только в том случае, если частные производные равны нулю.
дифференциал функции
равен нулю только в том случае, если частные производные равны нулю.
После
того, как стационарная точка ![]() найдена, необходимо
определить является ли она экстремальной, и если является, то какой именно -
точкой минимума или точкой максимума. Для ответа на этот вопрос нужно
исследовать поведение функции
найдена, необходимо
определить является ли она экстремальной, и если является, то какой именно -
точкой минимума или точкой максимума. Для ответа на этот вопрос нужно
исследовать поведение функции ![]() в окрестности
в окрестности ![]() .
.
Разложим функцию в ряд Тейлора:
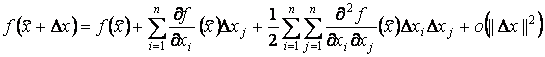 ,
,
где ![]() - некоторая норма вектора приращения, например, длина.
- некоторая норма вектора приращения, например, длина.
Поскольку
![]() , то
, то
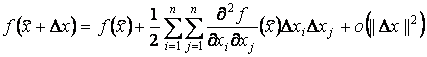 .
.
Вторые
производные сведем в матрицу, которая называется матрицей Гессе:
 .
.
Как
видим, характер стационарной точки ![]() по аналогии с
одномерным случаем зависит от знакоопределенности квадратичной формы
по аналогии с
одномерным случаем зависит от знакоопределенности квадратичной формы
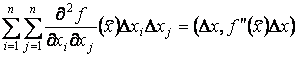 ,
,
где ![]() .
.
Определение
2. Квадратичная
форма и соответствующая ей матрица Гессе называются положительно
определенными в точке ![]() , если для любого
, если для любого ![]()
![]() ,
,
и
отрицательно определенными, если
![]() .
.
Теорема
4. (Достаточный признак). Для того чтобы дважды непрерывно дифференцируемая
функция ![]() имела в стационарной
точке
имела в стационарной
точке ![]() локальный минимум
(максимум) достаточно, чтобы матрица ее вторых производных в этой точке была
положительно (отрицательно) определенной.
локальный минимум
(максимум) достаточно, чтобы матрица ее вторых производных в этой точке была
положительно (отрицательно) определенной.
Критерий Сильвестра.
Необходимым и достаточным условием положительной определенности матрицы ![]()
![]() является выполнение
является выполнение ![]() условий:
условий:
![]() ,
, 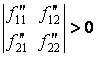 , … ,
, … ,  ,
,
т.е. необходимо
и достаточно, чтобы все главные диагональные миноры этой матрицы были положительны.
Необходимым и достаточным условием отрицательной
определенности матрицы является выполнение условий:
![]()
![]() ,
, ![]()
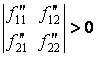 , … ,
, … , ![]()
 ,
,
т.е. необходимо и достаточно, чтобы
диагональные миноры нечетных порядков были
отрицательны, а четных положительны.
Пример 1. Исследуем
функцию 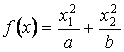 , где
, где ![]() .
.
Находим стационарную точку:

![]()
 .
.
Матрица Гессе:
 .
.
Диагональные миноры:
![]() ,
, 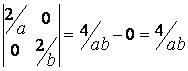 .
.
Возможны следующие исходы:
1)
если ![]() и
и ![]() , тогда оба минора положительны, матрица положительно
определена, следовательно, в стационарной точке минимум;
, тогда оба минора положительны, матрица положительно
определена, следовательно, в стационарной точке минимум;
2)
если ![]() и
и ![]() , тогда второй минор отрицателен, следовательно, экстремума
нет;
, тогда второй минор отрицателен, следовательно, экстремума
нет;
3)
если ![]() и
и ![]() , тогда второй минор отрицателен, следовательно, экстремума
нет;
, тогда второй минор отрицателен, следовательно, экстремума
нет;
4)
если ![]() и
и ![]() , тогда первый минор отрицателен, второй положителен, матрица
отрицательно определена, в стационарной точке максимум.
, тогда первый минор отрицателен, второй положителен, матрица
отрицательно определена, в стационарной точке максимум.