Задачи без ограничений. Необходимое

и достаточное условие экстремума

Пусть дана дважды непрерывно дифференцируемая функция одной переменной , где .

Определение 1. Точка называется точкой локального минимума (максимума) функции, если найдется некоторая окрестность этой точки, для всех точек которой выполняется условие:

> (<).

Определение 2. Точки локального максимума и минимума называются точками экстремума.

Теорема 1. (Необходимый признак экстремума функции.) Если точка является точкой экстремума функции, то производная в этой точке равна нулю или не существует.

Определение 3. Точки, в которых производная равна нулю или не существует, называются критическими.

Определение 4. Точки, в которых производная равна нулю, называются стационарными.

Теорема 2. (Первый достаточный признак экстремума.) Пусть - критическая точка и - некоторое положительное приращение аргумента. Тогда если то - точка локального минимума. Если же и то - точка локального максимума.

Теорема 3. (Второй достаточный признак экстремума.) Если в стационарной точке то - точка локального максимума, если то - точка локального минимума.

Рассмотрим функцию многих переменных, т. е. предположим, что аргументом функции является вектор , .

Определение 5. Точка называется точкой локального минимума (максимума) функции, если найдется некоторая окрестность этой точки, для всех точек которой выполняется условие:

> ( <)

Теорема 4. (Необходимый признак экстремума функции многих переменных.) Если точка является точкой экстремума функции, то частные производные в этой точке равны нулю или не существуют, т. е. если для всех

или не существует.

Точки, в которых все частные производные равны нулю, называются стационарными точками.

Пусть - стационарная точка. Найдем значения частных производных в этой точке и из полученных чисел составим матрицу (матрицу Гессе):

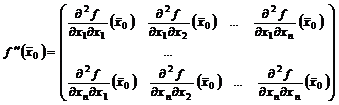
Определение 6. Матрица Гессе называется положительно (отрицательно) определенной, если для любого вектора приращения = справедливо соотношение ().

Теорема 5. (Достаточный признак экстремума функции многих переменных.) Для того чтобы дважды непрерывно дифференцируемая функция имела в стационарной точке локальный минимум (максимум), необходимо и достаточно, чтобы матрица Гессе в этой точке была положительно (отрицательно) определена.

Теорема 6. (Критерий Сильвестра.) Необходимым и достаточным условием положительной определенности матрицы Гессе является выполнение n условий:

,

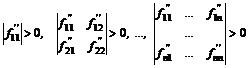т.е. необходимо и достаточно, чтобы все главные диагональные миноры этой матрицы были положительны. Необходимым и достаточным условием отрицательной определенности матрицы является выполнение следующих условий:

,

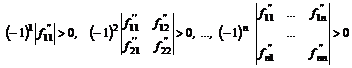т.е. необходимо и достаточно, чтобы миноры нечетных степеней были отрицательны, а миноры четных степеней положительны.

Пример 1. Исследовать на экстремум функцию

где.

Решение. Найдем частные производные функции и приравняем их к нулю:

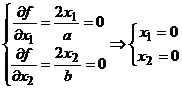
- стационарная точка.

Составим матрицу Гессе:

.

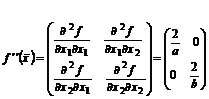
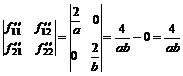1) Если a>0, b>0, тогда матрица положительно определена, следовательно, в стационарной точке минимум;

2) если a>0, b<0, второй минор отрицательный, экстремума нет;

3) если a<0, b>0, тогда первый и второй минор отрицательный, экстремума нет;

4) если a<0, b<0, тогда матрица отрицательно определена, следовательно, в стационарной точке максимум.