Оптимизация
- это выбор наилучшего варианта из множества возможных. Если критерий выбора
известен и вариантов немного, то решение может быть найдено путем перебора и
сравнения всех вариантов. Однако часто бывает так, что число возможных
вариантов настолько велико, что полный перебор практически невозможен. В таких
случаях приходится формулировать задачу на языке математики и применять
специальные методы поиска оптимального решения, т.е. методы оптимизации.
Все задачи оптимизации делятся на два больших класса: 1) задачи математического программирования и 2) задачи оптимального управления. Первые называют еще статическими задачами, а вторые динамическими. Если говорить кратко, то различие между этими классами задач состоит в том, что в задаче математического программирования необходимо найти оптимальное число (в общем случае вектор), а в задаче оптимального управления - оптимальную функцию. С формально-математической точки зрения, это различие существенное, но в прикладном плане оно зачастую оказывается весьма условным.
Далее мы будем рассматривать задачи математического программирования. Во-первых, потому, что именно к ним сводится большинство реальных задач планирования и управления в экономике; а во-вторых, потому, что многие задачи оптимального управления могут быть сформулированы при условии, что временная характеристика дискретна, и сведены таким образом к задачам математического программирования.
Задачи математического программирования:
классификация моделей и методов
В общем случае задача
математического программирования состоит в нахождении вектора ![]() , при котором достигается наибольшее или наименьшее значение
непрерывной скалярной функции
, при котором достигается наибольшее или наименьшее значение
непрерывной скалярной функции ![]() , при условии, что
, при условии, что ![]() , где
, где ![]() - допустимая область, представляющая собой некоторое
подмножество
- допустимая область, представляющая собой некоторое
подмножество ![]() -мерного евклидова пространства
-мерного евклидова пространства ![]() .
.
Математическая форма записи
этой задачи (для определенности сформулируем ее как задачу максимизации)
такова:
![]() . (1)
. (1)
Функцию ![]() называют целевой, а
условия, описывающие множество М, - системой ограничений. В зависимости от вида
этой функции и свойств допустимой области
называют целевой, а
условия, описывающие множество М, - системой ограничений. В зависимости от вида
этой функции и свойств допустимой области ![]() задача математического
программирования относится к тому или иному классу. Существуют различные
принципы классификации задач математического программирования.
задача математического
программирования относится к тому или иному классу. Существуют различные
принципы классификации задач математического программирования.
Наиболее важный
классификационный признак - выпуклость. По этому признаку все задачи математического
программирования разделяются на выпуклые и невыпуклые.
Определение 1. Задача математического программирования называется выпуклой, если
состоит в максимизации (минимизации) выпуклой вверх (вниз) целевой функции на
выпуклом множестве, в противном случае задача является невыпуклой.
Выпуклые задачи занимают
особое место среди прочих задач математического программирования. Чтобы решить
задачу (1), нужно найти все точки локальных
максимумов, а затем, сравнив значения целевой функции в них, определить
точку глобального максимума. В общем случае это очень сложная задача, поскольку
локальных максимумов может быть много и поиск каждого из них может быть
проблематичен. Однако если задача является выпуклой, то ситуация существенно
упрощается.
Теорема 1. В выпуклой задаче математического программирования
локальный экстремум одновременно является и
глобальным. Выпуклая задача математического программирования может иметь только
один строгий экстремум.
Если задача (1) выпуклая,
то, найдя точку локального экстремума, мы можем быть уверены, что нашли решение
или, по крайней мере, одно из решений.
Другой способ классификации
задач математического программирования основан на способах задания ограничений
задачи, т.е. множества ![]() Возможны следующие
варианты:
Возможны следующие
варианты:
1) ограничений может не быть
вообще;
2) они могут быть заданы
системой уравнений;
3) для задания ограничений могут использоваться
неравенства.
Определение 2. Если ![]() представляет собой
действительную непрерывно дифференцируемую
функцию и ограничения на переменные не накладываются (т.е.
представляет собой
действительную непрерывно дифференцируемую
функцию и ограничения на переменные не накладываются (т.е. ![]() =
=![]() ), то задача (1) называется классической задачей на экстремум
(безусловный экстремум).
), то задача (1) называется классической задачей на экстремум
(безусловный экстремум).
В основе решения задач такого вида лежит
теория дифференциального исчисления, в частности теория экстремумов, и
опирающиеся на нее методы.
Определение 3. Если ![]() представляет собой
действительную непрерывно дифференцируемую
функцию, а множество
представляет собой
действительную непрерывно дифференцируемую
функцию, а множество ![]() задано системой уравнений
задано системой уравнений
![]()
где ![]()
![]() - непрерывно дифференцируемые
скалярные функции,
- непрерывно дифференцируемые
скалярные функции, ![]() - действительные числа,
то задача (1) называется классической задачей на условный (относительный)
экстремум.
- действительные числа,
то задача (1) называется классической задачей на условный (относительный)
экстремум.
Эти задачи сводятся к задачам безусловной
оптимизации с помощью метода множителей Лагранжа. Поэтому для их решения и
анализа используется тот же аппарат, что и для задач на безусловный экстремум.
Нужно заметить, что авторы некоторых
учебников и монографий не относят классические задачи на экстремум к задачам
математического программирования, аргументируя это тем, что теория и методы их
решения появились задолго до появления самого термина "математическое
программирование". Если придерживаться такой трактовки, то задачами
математического программирования следует считать только такие задачи (1), в
системе ограничений которых содержатся неравенства. Задачи с ограничениями-неравенствами,
в свою очередь, принято делить на два класса - нелинейные и линейные.
Определение 4. Задача вида
![]()
![]() ,
,
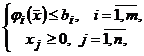
где ![]() и
и ![]()
![]() - непрерывно дифференцируемые
нелинейные, одновременно скалярные функции,
- непрерывно дифференцируемые
нелинейные, одновременно скалярные функции, ![]() - действительные
числа, называется задачей нелинейного программирования.
- действительные
числа, называется задачей нелинейного программирования.
Универсального и эффективного метода решения
задач нелинейного программирования (даже выпуклых, не говоря уже о невыпуклых)
не существует. Класс задач нелинейного программирования сам по себе довольно
обширен. В нем выделяют отдельные категории задач, имеющих ту или иную
специфику, позволяющую строить более эффективные, чем в общем случае,
алгоритмы. В качестве примера можно привести сепарабельные,
квадратичные, дробно-линейные задачи.
Определение 5. Если целевая функция задачи нелинейного программирования представима в
виде
![]() =
= ![]() +
+ ![]() + … +
+ … + ![]() ,
,
то задача называется задачей сепарабельного
программирования.
Определение 6. Если целевая функция ![]() задачи нелинейного
программирования представляет собой полином второй степени, а система
ограничений линейна, то задача называется задачей квадратичного
программирования.
задачи нелинейного
программирования представляет собой полином второй степени, а система
ограничений линейна, то задача называется задачей квадратичного
программирования.
Определение 7. Если целевая функция ![]() задачи нелинейного
программирования представляет собой дробно-линейную функцию, а система
ограничений линейна, то задача называется задачей дробно-линейного
программирования.
задачи нелинейного
программирования представляет собой дробно-линейную функцию, а система
ограничений линейна, то задача называется задачей дробно-линейного
программирования.
Определение 8. Если ![]() представляет собой
линейную функцию, а множество
представляет собой
линейную функцию, а множество ![]() задается с помощью
системы линейных уравнений и неравенств, то задача (1) называется задачей
линейного программирования.
задается с помощью
системы линейных уравнений и неравенств, то задача (1) называется задачей
линейного программирования.
Линейное программирование принято
рассматривать как самостоятельный раздел математического программирования ввиду
той особой роли, которую оно играет в экономической теории и практике.
Линейное программирование имеет развитую
теорию. Существует много эффективных методов решения задач линейного
программирования. Кроме того, существуют приемы, позволяющие расширить область
применения методов решения задач линейного программирования. Некоторые задачи
математического программирования, формально не относящиеся к линейным, могут
быть преобразованы и решены методами, используемыми для решения линейных задач.
Это относится, например, к задачам дробно-линейного программирования.
Важную роль в теории и
практике математического программирования играют также задачи целочисленного
(дискретного) программирования.
Определение 9. Если на переменные задачи (1) накладывается условие целочисленности,
то она называется задачей целочисленного программирования.
В экономике большое число
задач носит целочисленный характер. Это связано с физической неделимостью
многих объектов расчета. Но интерес к целочисленному программированию
обусловлен еще и тем, что многие нелинейные невыпуклые задачи могут быть
сведены к задачам линейного программирования с дополнительным требованием целочисленности. Теория целочисленного программирования
используется также для разработки методов решения комбинаторных задач, например
для составления расписаний.
Перейдем к рассмотрению
методов решения задач математического программирования. Методы, которые
применяют для решения задач математического программирования, не менее
разнообразны, чем модели. Как правило, метод решения определенного класса задач
имеет несколько модификаций. Например, для решения задач линейного
программирования используют симплекс-метод. Кроме простого симплекс-метода,
существуют еще симплекс-метод с обратной матрицей, двойственный симплекс-метод,
метод последовательного сокращения невязок и ряд других модификаций.
Вместе с тем между моделями
и методами нет взаимно однозначного соответствия. Одна и та же задача может
решаться разными методами, и один и тот же метод может быть использован для
решения задач, относящихся к разным категориям.
Несмотря на разнообразие,
все методы решения задач математического программирования имеют некоторые общие
черты. Во-первых, практически все они являются численными. То есть представляют
собой алгоритмы, ориентированные на компьютерную реализацию. Во-вторых, любой
алгоритм, как бы он ни был сложен или оригинален, представляет собой реализацию
одного из трех основных принципов:
· последовательное
приближение;
· последовательный анализ
вариантов;
· случайный поиск.
Большинство методов решения задач математического программирования основаны на принципе последовательного приближения: в некоторой точке пространства переменных определяется допустимое направление возрастания (или убывания - в зависимости от постановки задачи) целевой функции и делается шаг в этом направлении. Затем анализируется результат, т.е. проверяется, не является ли новая точка искомым решением. Если нет, то вся процедура повторяется вновь. По этому принципу построены, например, градиентные методы, а также один из наиболее часто применяемых и эффективных методов математического программирования - симплексный метод. Как правило, методы этой группы очень эффективны. Недостаток этих методов состоит в том, что они могут найти только локальный экстремум. Если задача невыпуклая (многоэкстремальная), то мы не будем иметь гарантию, что найденное таким способом решение действительно оптимально.
Другую группу составляют методы последовательного анализа вариантов. Сюда относятся такие известные методы, как динамическое программирование, метод ветвей и границ и ряд других. Содержанием этих методов является построение правил отбраковки подмножеств допустимых вариантов, среди которых не может содержаться оптимального решения. Сама эта процедура, как правило, существенно учитывает специфику задачи. Поэтому здесь трудно разработать стандартные алгоритмы, которые могли бы применяться для решения широкого круга прикладных задач. Но зато эти методы могут быть использованы для решения невыпуклых и комбинаторных задач.
Еще один
возможный принцип, лежащий в основе методов решения задач математического
программирования, - случайный поиск: формируется некоторый случайный вариант
решения (для этого используются компьютерные программы, генерирующие псевдослучайные
числа) и вычисляется соответствующее значение целевой функции. Новый вариант
сравнивается с лучшим, из ранее достигнутых. Если сравнение в пользу нового
варианта, то он запоминается вместо того, который был раньше, и процедура
повторяется. Эффективность метода определяется скоростью, с которой компьютер
генерирует и оценивает варианты. А это обычно происходит очень быстро. Кроме
того, сама процедура генерирования вариантов может быть не совсем случайной, а
лишь носить элемент случайности. Но, разумеется, гарантии нахождения оптимума
нет. Поэтому эти методы применяют лишь тогда, когда нет более надежных и
эффективных; а также в тех нередких на практике случаях, когда нужно найти не
обязательно оптимальный, а хотя бы достаточно хороший результат.