Градиент функции многих переменных

Рассмотрим функцию трех переменных n = 3, u = f(x, y, z).

Определение 1. Градиентом функции многих переменных в данной точке называется вектор, координаты которого равны частным производным по соответствующим аргументам, вычисленным в данной точке.

.

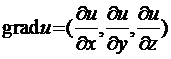Теорема 1. Производная функции в данном направлении равна проекции градиента на данное направление.

Доказательство. Даны функция u = f(x,y,z) и некоторое направление , заданное направляющими косинусами .

Единичный вектор данного направления — .

Производная по направлению в данной точке равна

,

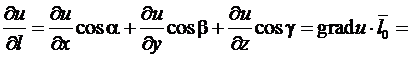
где j — угол между градиентом и направлением (рис. 1).

Рис. 1

.

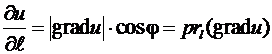Следствие. Градиент функции в данной точке показывает направление наискорейшего возрастания функции. Модуль градиента совпадает с максимальной скоростью возрастания функции в данной точке.

Доказательство. Из теоремы следует, что

.

Выясним, в каком из направлений в данной точке функция растет быстрее всего. Максимум будет достигаться, когда , т.е. направление совпадает с направлением градиента.

.

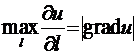Рассмотрим функцию двух переменных n = 2, .

Теорема 2. Градиент функции в каждой точке области определения направлен по нормали к линии уровня (нормалью к плоской кривой называется перпендикуляр к касательной, проведенной в точку касания).