Связь дифференцируемости

и непрерывности функции

Имеет место следующая теорема. Если функция дифференцируема в точке , то она непрерывна в этой точке.

Доказательство. Так как функция дифференцируема в точке , то существует конечный предел . Тогда по теореме о связи бесконечно малой с функцией, имеющей конечный предел, будем иметь

,

где - бесконечно малая величина при .

Откуда

.

Переходя в этой формуле к пределу при , получим по свойствам бесконечно малых, что .

Следовательно, по одному из определений непрерывности функция в точке является непрерывной.

Обратная теорема, вообще говоря, неверна, т.е. функция может быть непрерывной в данной точке, но не быть дифференцируемой в этой точке.

В качестве примера исследуем функцию в точке , которая непрерывна в точке (впрочем, как и во всех других точках числовой прямой). В этой точке ее левосторонний и правосторонний пределы равны нулю, что совпадает со значением самой функции в точке .

По определению

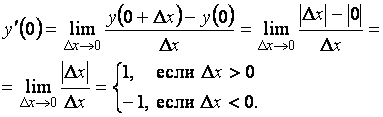
Таким образом, функция в точке имеет конечные, но не равные друг другу односторонние производные (левая равна , а правая равна ). Поэтому она не имеет производной в этой точке и не является в ней дифференцируемой.