Задача потребительского выбора

В теории потребления предполагается, что потребитель всегда стремится максимизировать свою полезность и ограничением для него является величина дохода I, которую он может потратить на приобретение набора товаров. В общем, задача потребительского выбора (задача рационального поведения потребителя на рынке) записывается следующим образом: найти такой потребительский набор

,

который максимизирует его функцию полезности при заданном бюджетном ограничении. Задачу потребительского выбора можно записать в виде

,

Задачу потребительского выбора рассмотрим для случая набора из двух товаров: найти такой набор , для которого

I,

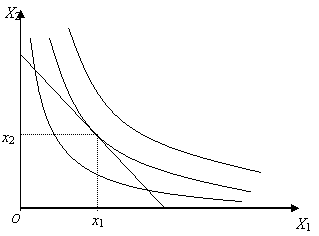
Рис. 1

Поиск оптимального набора графически можно изобразить как последовательный переход на кривые безразличия более высокого уровня полезности (рис. 1) вправо и вверх до тех пор, пока эти кривые имеют общие точки с бюджетным множеством. Из рис. 1 следует, что искомая точка лежит на границе G, т.е. на прямой I.

Таким образом, задача потребительского выбора сводится к задаче на условный экстремум функций двух переменных: найти точку , для которой

I.

Исходя из бюджетного множества n-мерных наборов В следует, что точка лежит на границе G и удовлетворяет условию I. Поэтому задача потребительского выбора формулируется аналогично в виде задачи на условный экстремум: при заданных функции, векторе и величине I найти такую точку, что

I.

Второе уравнение выражения называется уравнением связи.

Решение задачи потребительского выбора

Для решения задачи

I.

используем метод Лагранжа. Составим функцию Лагранжа:

, (1)

где l - множитель Лагранжа.

Из (1) следует экономический смысл множителя Лагранжа: если цены и доход меняются в одно и то же число раз l, то функция полезности и решение задачи потребительского выбора не изменятся. Для нахождения максимума функции L приравняем к нулю все три частные производные этой функции, получим систему уравнений:

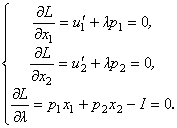
Исключив из этих уравнений l, получим систему двух уравнений с неизвестными x₁, x₂:

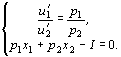
Из системы находится точка - решение задачи потребительского выбора.

Метод Лагранжа используется и для решения многомерной задачи потребительского выбора.

Составим функцию Лагранжа:

.

Для нахождения максимума функции L приравняем к нулю все частные производные этой функции, получим систему уравнений:

,

Исключив из уравнений множитель l, получим систему:

(2)

Решение системы - точка условного экстремума. Это решение общей задачи потребительского выбора.

Точка называется точкой локального рыночного равновесия. Первое выражение системы (2) показывает, что отношение предельных полезностей продуктов в точке локального рыночного равновесия, или предельная норма замены i-го продукта j-м продуктом , равно отношению рыночных цен на эти продукты.