Задача на безусловный экстремум

Оптимизация — это выбор наилучшего варианта из множества возможных. Если критерий выбора известен и вариантов не много, то решение может быть найдено простым перебором и сравнением всех вариантов. Однако часто бывает так, что количество возможных вариантов велико и перебор практически невозможен. Тогда приходится формализовать задачу, составлять ее математическую модель и применять специальные методы поиска наилучшего решения.

Среди множества оптимизационных задач выделяют группу классических задач оптимизации или задач на безусловный экстремум. Общая постановка этих задач такова: найти вектор , при котором достигается наибольшее или наименьшее значение скалярной непрерывно дифференцируемой функции :

.

В основе методов решения классических задач оптимизации лежит теория дифференциального исчисления.

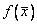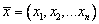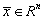Пусть — действительная дважды непрерывно дифференцируемая функция аргумента , . Требуется найти наибольшее (или наименьшее) значение данной функции и такое значение аргумента 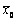(оптимальное решение), при котором этот экстремум достигается.

Если точка является точкой экстремума функции, то она является стационарной точкой функции, т.е. частные производные в этой точке равны нулю:

, .

Таким образом, экстремумы функции следует искать среди ее стационарных точек. Однако, возможно, не каждая стационарная точка является точкой экстремума.

Для решения вопроса о наличии экстремума функции многих переменных в стационарной точке находят значения вторых частных производных в этой точке и из полученных чисел составляют матрицу, называемую матрицей Гессе:

.

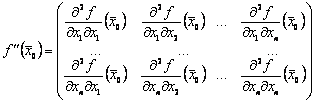Для того чтобы функция имела в стационарной точке локальный минимум, необходимо и достаточно, чтобы в этой точке все главные диагональные миноры матрицы Гессе были положительны.

Для того чтобы функция имела в стационарной точке локальный максимум, необходимо и достаточно, чтобы у матрицы Гессе главные диагональные миноры нечетных степеней были отрицательны в этой точке, а миноры четных степеней — положительны.