Несобственные интегралы второго рода

Если функция не ограничена на промежутке интегрирования и промежуток интегрирования конечен, то определенный интеграл является несобственным интегралом второго рода.

1. Пусть функция y = f(x) определена и непрерывна на [a,b) и в окрестности точки b функция не ограничена (рис. 1).

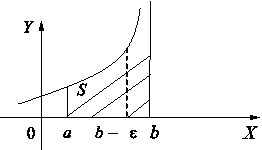
Рис. 1

.

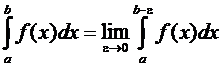Если предел, стоящий справа, существует и конечен, то несобственный интеграл называется сходящимся и равен значению этого предела, в противном случае интеграл называется расходящимся.

Если F(x) — первообразная функции, то

.

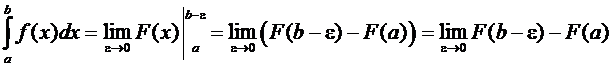Пример 1. Вычислить несобственный интеграл от функции 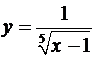по промежутку [0, 1) (рис. 2).

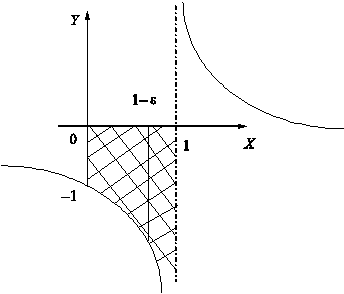
Рис. 2

.

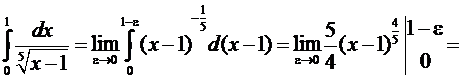
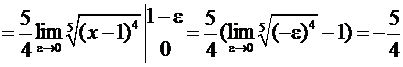Несобственный интеграл сходится.

2. Аналогично определяются интегралы второго рода в других ситуациях: y = f(x) определена и непрерывна на (a,b] и в окрестности точки а не ограничена (рис. 3).

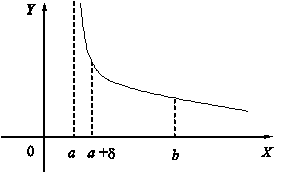
Рис. 3

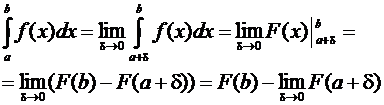
3. Пусть функция y = f(x) определена и непрерывна на [a,c) È (c,b] и в окрестности точки с функция неограниченна (рис. 4).

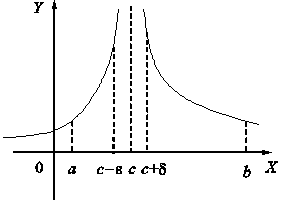
Рис. 4

.

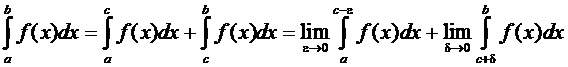Если оба предела, стоящие в правой части, существуют и конечны, то несобственный интеграл называется сходящимся и он равен сумме этих пределов, в противном случае — расходящимся.

Замечание 1. Несобственные интегралы могут быть комбинированного типа: первого и второго рода; или второго рода с несколькими точками разрыва второго рода.

Замечание 2. Если функция на отрезке интегрирования терпит разрыв первого рода в точке с, то определенный интеграл от нее по этому отрезку не является несобственным, так как его можно свести к сумме двух обычных определенных интегралов (рис. 5).

Рис. 5

.
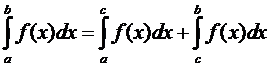