Связь между непрерывностью

и дифференцируемостью функции

Теорема (необходимое условие дифференцируемости функции). Если функция дифференцируема в точке, то она непрерывна в этой точке.

Доказательство. Пусть функция у=f(x) дифференцируема в точке х₀. Дадим в этой точке аргументу приращение Dх. Функция получит приращение Dу. Найдем .

.

Следовательно, у=f(x) непрерывна в точке х₀.

Следствие. Если х₀ – точка разрыва функции, то в ней функция не дифференцируема.

Утверждение, обратное теореме, не верно. Из непрерывности не следует дифференцируемость.

Пример. у=|х| , х₀=0.

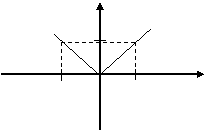Y

0 X

Dх>0, ;

Dх<0, .

В точке х₀=0 функция непрерывна, но производной не существует.