Применение функций в экономике

Производственные функции

Рассмотрим некоторую производственную систему.

Определение. Функция, выражающая зависимость объема производства от величины затраченных ресурсов, называется производственной.

Существует целое семейство производственных функций. Рассмотрим производственную функцию

y=f(x),

где х – суммарная величина затрат в стоимостном выражении, у – суммарный выпуск в стоимостном выражении. По своему экономическому смыслу, х³0 и у³0. Производственная функция отражает существующую технологию: изменение технологии ведет к изменению производственной функции.

Если предположить, что производственная функция строго возрастает, т.е. любое увеличение затрат ведет к увеличению выпуска, то производственная функция имеет обратную функцию x=f^--1(y), которая определяет величину производственных затрат х, необходимых для выпуска объема у. Эта функция называется функцией затрат. Она будет строго возрастающей.

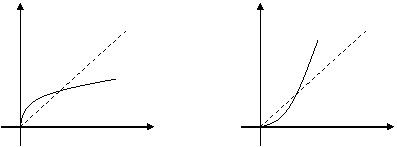
Y X

x=f^{- -1}(y)

y=f(x)

0 X 0 Y

Кривые спроса и предложения. Точка равновесия

Рассмотрим функцию зависимости спроса D от цены на товар P. Чем меньше цена, тем больше спрос при постоянной покупательной способности населения. Обычно зависимость D от Р имеет вид ниспадающей кривой:

D=kP^a+c, где а < 0.

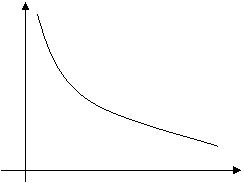D

0 P

Рассмотрим функцию предложения S от цены на товар P. Предложение растет с увеличением цены на товар. Зависимость S от Р имеет следующий вид:

S=P^b+d, где b ³ 1.

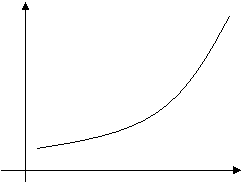S

0 P

Параметры c и d - так называемые экзогенные величины; они зависят от ряда причин (благосостояние общества, политическая обстановка и т.п.). Переменные, входящие в формулы, положительны, поэтому графики функций имеют смысл только в первой координатной четверти.

Для экономики представляет интерес условие равновесия, т.е. когда спрос равен предложению. Такое условие задается уравнением

и соответствует точке пересечения кривых D и S - это так называемая точка равновесия (точка М₁). Цена Р₀, при которой выполняется данное условие, называется равновесной.

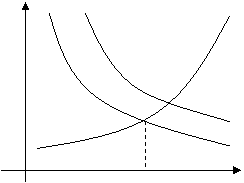D, S D₁ D₂ S

M₂

M₁

0 P₀ P

При увеличении благосостояния населения, что соответствует росту величины с, точка равновесия М₁ смещается вправо, так как кривая D поднимается вверх; при этом цена на товар растет при неизменной кривой предложения S.

Паутинная модель рынка

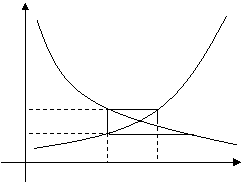
Рассмотрим простейшую задачу поиска равновесной цены. Это одна из основных проблем рынка, означающая фактический торг между производителем и покупателем.

Пусть сначала цену P₁, называет производитель (в простейшей схеме он же и продавец). Цена P₁ на самом деле выше равновесной (естественно, всякий производитель стремится получить максимум выгоды из своего производства). Покупатель оценивает спрос D₁ при этой цене, находит его низким и называет свою цену P₂, при которой спрос D₁ равен предложению. Цена P₂ ниже равновесной (всякий покупатель стремится купить дешевле). В свою очередь производитель оценивает спрос D₂, соответствующий цене Р₂, и определяет свою цену Р₃, при которой спрос равен предложению, эта цена выше равновесной.

D, S D S

D₂

D₁

0 P₂ P₀ P₃ P₁ P

Процесс торга в итоге приводит к приближению к равновесной цене, т.е. к "скручиванию" спирали (паутине). Если рассматривать последовательность чисел, состоящую из называемых в процессе торга цен, то она имеет своим пределом равновесную цену Р₀.