Применение функций нескольких переменных в экономике

Коэффициенты эластичности

В реальных случаях спрос на товар может зависеть от многих факторов, т.е. спрос – это функция нескольких переменных.

Пусть функция - функция спроса на некоторый товар Q, которая зависит от цены Р, доходов потребителей I и цены альтернативного товара Р_А. Интерес представляет процесс изменения спроса при изменении цен и доходов. Количественный ответ дается с помощью понятия эластичности.

Эластичность спроса относительно цены (собственной) вычисляется по формуле

, (1)

где цена альтернативного товара Р_А и доходы I постоянны.

Перекрестная эластичность спроса относительно цены определяется как

, (2)

где постоянными считаются собственная цена товара Р и доход I.

Заметим, что знак этого коэффициента может принимать как положительные, так и отрицательные значения.

Если альтернативный товар относится к взаимозаменяемым, то , так как рост цены альтернативного товара приводит к увеличению спроса (потребители отдают предпочтение менее дорогому товару), т.е.

.

Если альтернативный товар относится к взаимодополняющим, то , так как рост цены альтернативного товара приводит к уменьшению спроса (общие затраты на приобретение двух видов товаров увеличиваются), т.е.

.

Эластичность спроса относительно дохода выражается формулой

, (3)

где цены самого товара и альтернативного представляют собой постоянные величины.

Заметим, что для качественных товаров спрос увеличивается с ростом доходов, т.е. , а для низкосортных товаров он уменьшается, т.е. .

Пример 1. Функция спроса на некоторый товар определяется формулой . Найти эластичность спроса относительно собственной цены товара, перекрестную эластичность спроса относительно цены и эластичность спроса относительно дохода, если цена товара , цена альтернативного товара , а доход .

Решение. Величина спроса

.

Частная производная по Р примет вид

.

Зная формулу эластичности спроса относительно цены

,

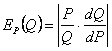получим

.

Частная производная по Р_А примет вид

.

Зная формулу перекрестной эластичности спроса относительно цены

,

получим

.

Коэффициент положительный, следовательно, товары взаимозаменяемы.

Частная производная по I примет вид

.

Зная формулу эластичности относительно дохода

,

получим

.

Положительный знак эластичности показывает, что с ростом дохода спрос на товар будет увеличиваться.

Потребительский выбор

Определение. Потребительским выбором называется набор определенного количества благ потребителя, сделанный с учетом структуры цен, дохода и собственных предпочтений.

Определение. Потребителький набор – это вектор , координата х₁ которого равна количеству единиц первого товара, а координата х₂ равна количеству второго товара.

На множестве потребительских наборов определена функция - функция полезности потребителя. Ее значение на потребительском наборе равно личностной оценке потребителя этого набора.

Определение. Потребительская оценка набора называется уровнем (или степенью) удовлетворения потребностей личности при приобретении или потреблении им данного набора .

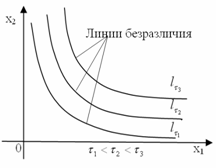
Определение. Линия, соединяющая потребительские наборы , имеющие одинаковый уровень удовлетворения потребностей личности, называется кривой безразличия (изоквантой).

Рис. 1

Рис. 2

Линия безразличия (рис. 1) - это линия уровня функции полезности.

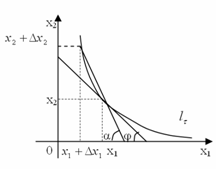
Заметим, что точки , принадлежат одной и той же линии безразличия (рис. 2). Поэтому дробь называют нормой замены первого товара вторым в потребительском наборе , а производную , равную предельному значению дроби при , - предельной нормой замены первого товара вторым.

Рациональное поведение потребителя на рынке заключается в выборе потребительского набора , который максимизирует его функцию полезности при заданном бюджетном ограничении.

Бюджетное ограничение означает, что денежные расходы на блага не могут превышать денежного дохода, т.е. , где р₁ и р₂ - рыночные цены одной единицы первого и второго благ, соответственно, а I – доход потребителя, который он готов потратить на приобретение этих благ.

Пусть функция полезности потребителя. Найти такой набор , который максимизирует функцию полезности при . Для решения этой задачи на условный экстремум применим метод Лагранжа.

Запишем функцию Лагранжа: . Найдем ее частные производные первого порядка по переменным х₁, х₂ и λ, приравняем их к нулю:

, , .

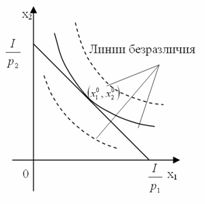
Получим систему уравнений с двумя переменными:

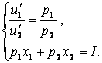
Решение системы - это критическая точка функции Лагранжа (точка локального рыночного равновесия), которая является решением задачи потребительского выбора.

Рис. 3

Геометрически решение можно интерпретировать как точку касания линии безразличия функции полезности с бюджетной прямой (рис. 3). Заметим, что частные производные , по переменным х1 и х2 получили название предельных полезностей.

Предельные полезности являются убывающими функциями по соответствующим переменным, т.е. по мере роста количества приобретаемого товара каждая следующая единица товара приносит меньше удовольствия потребителю. При незначительных изменениях переменных х₁ и х₂ можно приближенно получить изменение полезности по следующей формуле:

. (4)

Пример 2. Функция полезности двух товаров задана формулой

.

Определить изменение полезности товаров, если х₁ уменьшается от 100 до 99, а х₂ увеличивается от 200 до 201.

Решение. Зная формулу изменения полезности

,

найдем частные производные по переменным х₁ и х₂:

, .

Подставив и , получим численные значения частных производных:

, .

Численные значения приращения независимых переменных

, .

Подставив значения в формулу, приближенно найдем изменение полезности

.

Пример 3. Фирма производит два вида товаров и продает их по цене 1000 и 800 соответственно. Найти объемы выпуска товаров х и у, при которых прибыль была бы максимальной, если функция издержек имеет вид .

Решение. Суммарный доход от продажи обоих товаров: . Прибыль представляет собой разницу между доходом и затратами:

,

или

- функция, максимум которой надо найти.

Найдем частные производные первого порядка по переменным х и у, приравняем их к нулю:

, .

Получим систему уравнений с двумя переменными:

Точка - критическая точка исследуемой функции. Согласно достаточному условию экстремума определим статус данной точки. Для этого вычислим частные производные второго порядка:

, , ;

найдем

,

где

, .

При объемах производства двух видов товаров функция достигает максимальной прибыли:

.

Производственная функция

Определение. Производственной функцией нескольких переменных называется функция, независимые переменные которой принимают значения объемов затрачиваемых или используемых ресурсов (число переменных n равно числу ресурсов), а значение функции определяет величины объемов выпуска:

. (5)

Пусть - производственная функция. Дробь

- средняя производительность i-го ресурса;

- предельная (маржинальная) производительность i-го ресурса;

- предельная норма замены i-го ресурса j-м при сохранении объема выпуска у, где i – номер заменяемого ресурса, j - номер замещающего ресурса.

Определение. Отношение предельной производительности i-го ресурса к его средней производительности называется (частной) эластичностью выпуска по i-му ресурсу, т.е.

. (6)

Сумма

представляет собой эластичность производства.

Определение. Коэффициентом эластичности замещения называется величина

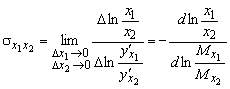. (7)

Величина , обратная коэффициенту эластичности замещения, показывает приближенно, на сколько процентов изменится отношение предельных продуктов при изменении отношения затрат ресурсов на 1%.

Прибыль от производства разных товаров

Пусть - количества производимых m разновидностей товара, а , соответственно, их цены ( - постоянные величины). Найти прибыль производства, если затраты на производство этих товаров задаются функцией издержек .

Функция прибыли имеет вид

. (8)

Тогда максимум прибыли ищется как условие локального экстремума функции нескольких переменных при :

.

Данное условие приводит к системе алгебраических уравнений относительно переменных :

Заметим, что полученная система уравнений реализует правило экономики: предельная стоимость товара равна предельным издержкам на производство этого товара.

Решениями данной системы уравнений являются m-мерные точки.

Пример 4. Производится х ед. первого товара по цене Р₁ = 9 ден. ед. и у ед. второго товара по цене Р₂ = 12 ден. ед. Найти прибыль от производства данных товаров по формуле

.

Решение. Согласно условиям локального экстремума

:

, ,

получим систему линейных алгебраических уравнений:

откуда

Так как

, , ,

имеем

, .

Следовательно, точка является локальным максимумом функции прибыли:

ден. ед.

Оптимальное распределение ресурсов

Пусть функция выпуска имеет вид при условии, что функция затрат на ресурсы х и у линейна, т.е. , где р₁ и р₂ - цены на ресурсы. Найти оптимальное распределение ресурсов при выпуске продукции.

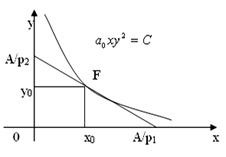
В точке оптимального распределения ресурсов линии уровня функций выпуска и затрат касаются (рис. 4).

Рис. 4

Данные линии определяются следующими линиями: , , или , , где и - постоянные числа, . Значение х0 найдем из условия касания указанных линий, которое определяется уравнением

, откуда .

Из приведенного уравнения значение . Из уравнения линии уровня функции выпуска определим значение . Получаем, что оптимальное распределение ресурсов должно быть произведено в отношении .

Пример 5. Определить оптимальное распределение ресурсов для функции выпуска , если затраты на факторы х и у - линейны и задаются ценами р₁ = 1, р₂ = 2.

Решение. В точке (х₀;у₀), задающей оптимальное распределение ресурсов х и у, линия уровня функции издержек касается линии , откуда

.

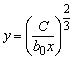Линия уровня функции издержек - это прямые , угловой коэффициент которых .

Условие касания имеет вид

,

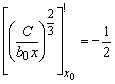откуда

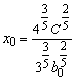и соответственно .

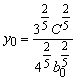Таким образом, факторы х, у следует распределить в отношении 4:3.

Пример 6. Имеются следующие данные о цене на нефть х, ден. ед., и индексе акций нефтяных компаний у, усл. ед.

х	17,28	17,05	18,30	18,80	19,20	18,50
у	537	534	550	555	560	552

Предполагая, что между переменными х и у существует линейная зависимость, найти эмпирическую формулу вида , используя метод наименьших квадратов.

Решение. Найдем необходимые для расчетов суммы

, , ,.

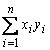Промежуточные вычисления оформим в виде вспомогательной таблицы:

xi	yi	xiyi	xi^2
17,28	537	9279,36	298,5984
17,05	534	9104,70	290,7025
18,30	550	10065,00	334,8900
18,80	555	10434,00	353,4400
19,20	560	10752,00	368,6400
18,50	552	10212,00	342,2500
Σ 109,13	3288	59847,06	1988,5209

Система нормальных уравнений

имеет вид

откуда

Получим искомую зависимость: y = 12,078x+328,32. Таким образом, с увеличением цены нефти на 1 ден. ед. индекс акций нефтяных компаний в среднем растет на 12,08 ед.