Задачи с ограничениями-уравнениями.
Функция Лагранжа
Исследуем
на экстремум функцию ![]() , при условии, что вектор
, при условии, что вектор ![]() удовлетворяет
уравнениям связи
удовлетворяет
уравнениям связи ![]() где
где ![]() - дважды непрерывно
дифференцируемые скалярные функции векторного аргумента. Предположим, что
- дважды непрерывно
дифференцируемые скалярные функции векторного аргумента. Предположим, что ![]() - решение задачи
- решение задачи
![]() . (1)
. (1)
В
этом случае говорят, что ![]() является точкой условного
максимума функции
является точкой условного
максимума функции ![]() .
.
Определение 1. Допустимая точка ![]() есть точка условного
максимума функции
есть точка условного
максимума функции ![]() , если существует такое
, если существует такое ![]() , что для всех
, что для всех ![]() , удовлетворяющих уравнениям связи и условию
, удовлетворяющих уравнениям связи и условию ![]() , выполняется неравенство
, выполняется неравенство
![]() .
.
В
принципе, уравнения связи можно было бы использовать для того, чтобы в
некоторой окрестности допустимой точки какие-либо ![]() переменных выразить
через остальные
переменных выразить
через остальные ![]() :
:
![]() . (2)
. (2)
Это возможно, если в рассматриваемой точке существуют частные производные и определитель матрицы частных производных (якобиан) не равен нулю,
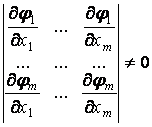 . (3)
. (3)
Тогда
подставляя (2) в целевую функцию ![]() , можно свести исходную задачу к отысканию безусловного
экстремума функции
, можно свести исходную задачу к отысканию безусловного
экстремума функции ![]() переменных
переменных
![]() .
.
Функция Лагранжа. Однако
осуществить такой подход напрямую чаще всего бывает трудно или даже невозможно.
Рассмотрим другой путь, который не предполагает использования явных выражений
(2), хотя и опирается на условие (3). Он связан с так называемой функцией Лагранжа
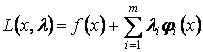 , (4)
, (4)
где ![]() - множители Лагранжа.
- множители Лагранжа.
Теорема 1. Пусть точка ![]() - решение задачи (1),
и в ее окрестности выполняется условие (3). Тогда существует вектор
- решение задачи (1),
и в ее окрестности выполняется условие (3). Тогда существует вектор ![]() такой, что
такой, что ![]() представляет собой
стационарную точку функции Лагранжа.
представляет собой
стационарную точку функции Лагранжа.
Доказательство. В стационарной точке ![]() полный дифференциал равен нулю. Запишем это с
учетом разделения переменных на зависимые и
независимые:
полный дифференциал равен нулю. Запишем это с
учетом разделения переменных на зависимые и
независимые:
 , (5)
, (5)
где
![]() - дифференциалы
зависимых переменных, связанные с дифференциалами
- дифференциалы
зависимых переменных, связанные с дифференциалами ![]() независимых переменных
системой уравнений
независимых переменных
системой уравнений
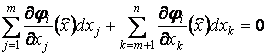 ,
, ![]() . (6)
. (6)
Исключим
дифференциалы зависимых переменных из уравнений (5), (6). Для этого умножим
каждое из уравнений системы (6) на произвольные множители ![]()
![]()
![]() . Результаты сложим с уравнением (5):
. Результаты сложим с уравнением (5):
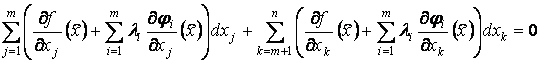 . (7)
. (7)
Подберем
множители ![]()
![]()
![]() так, чтобы
коэффициенты при дифференциалах зависимых переменных стали нулевыми:
так, чтобы
коэффициенты при дифференциалах зависимых переменных стали нулевыми:
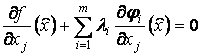 ,
, ![]() , (8)
, (8)
Перепишем
эти условия в несколько ином виде:
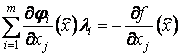 ,
, ![]() .
.
Получили
систему линейных уравнений относительно ![]() . Эта система имеет единственное решение, поскольку
предполагается, что ее определитель не равен нулю (см. условие (3)).
. Эта система имеет единственное решение, поскольку
предполагается, что ее определитель не равен нулю (см. условие (3)).
При
выбранных таким образом множителях ![]() в выражении (7)
останутся лишь члены, содержащие дифференциалы независимых переменных.
в выражении (7)
останутся лишь члены, содержащие дифференциалы независимых переменных.
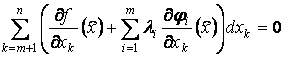 .
.
Из
чего в силу произвольности ![]() следует, что
следует, что
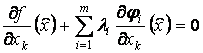 ,
, ![]() . (9)
. (9)
Таким
образом, мы получили систему ![]() уравнений относительно
переменных
уравнений относительно
переменных ![]() . Это уравнения связи,
. Это уравнения связи, ![]() а также уравнения (8)
и (9). Как видим, они совпадают с условиями стационарности функции Лагранжа:
а также уравнения (8)
и (9). Как видим, они совпадают с условиями стационарности функции Лагранжа:
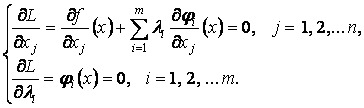
Теорема
доказана.
К
такому же выводу можно прийти, если рассмотреть геометрическую интерпретацию
задачи двух переменных
![]() ,
, ![]() . (10)
. (10)

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рис. 1.
Графическое представление задачи
Предположим,
что целевая функция представлена совокупностью изоквант
(линий постоянного уровня) ![]() , где
, где ![]() (Рис. 1). Очевидно,
найдется изокванта, которая будет иметь с кривой
(Рис. 1). Очевидно,
найдется изокванта, которая будет иметь с кривой ![]() точку касания
точку касания ![]() . Эта точка и будет решением задачи, поскольку смещение из
нее по допустимой линии в любом направлении приводит к попаданию на изокванты более низкого уровня. Заметим, что в этой точке
кривые
. Эта точка и будет решением задачи, поскольку смещение из
нее по допустимой линии в любом направлении приводит к попаданию на изокванты более низкого уровня. Заметим, что в этой точке
кривые ![]() и
и ![]() имеют совпадающие
касательные. Следовательно, их градиенты,
лежат на одной прямой и отличаются на постоянный множитель:
имеют совпадающие
касательные. Следовательно, их градиенты,
лежат на одной прямой и отличаются на постоянный множитель:
![]() . (11)
. (11)
Таким
образом, в точке ![]() выполняются условия
(1) и (11), но это и есть условия стационарности функции Лагранжа для данной
задачи, т.е. функции
выполняются условия
(1) и (11), но это и есть условия стационарности функции Лагранжа для данной
задачи, т.е. функции
![]() .
.
Метод множителей Лагранжа. Итак,
используя функцию Лагранжа, задачу с ограничениями, заданными с помощью
уравнений, можно свести к безусловной задаче. Метод включает следующие этапы:
1.
Составляем функцию Лагранжа
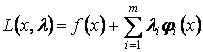 .
.
2. Выписываем необходимые условия:
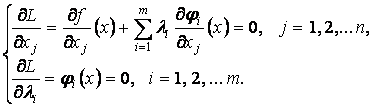
3.
Решаем полученную систему уравнений, находим условно-стационарную точку ![]() ,
,![]() . Заметим, что для решения этой системы, возможно,
потребуется использование численных методов, изложение которых дано ниже.
. Заметим, что для решения этой системы, возможно,
потребуется использование численных методов, изложение которых дано ниже.
4. Анализируем выполнение достаточных условий,
проверяем знакоопределенность квадратичной формы функции Лагранжа
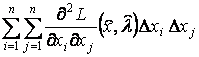 .
.
Если
получается отрицательный результат, то анализ следует провести для векторов ![]() , удовлетворяющих системе линейных уравнений
, удовлетворяющих системе линейных уравнений
 ,
, ![]() ,
,
которые образуются в результате
дифференцирования уравнений связи. Поскольку выполняется условие (3), то можно
выразить m переменных через остальные ![]() и подставить
полученные выражения в квадратичную форму. Затем квадратичную форму,
определяемую теперь уже только независимыми приращениями, нужно вновь
исследовать на знакоопределенность.
и подставить
полученные выражения в квадратичную форму. Затем квадратичную форму,
определяемую теперь уже только независимыми приращениями, нужно вновь
исследовать на знакоопределенность.
Пример 1. Исследуем на экстремум функцию ![]() при условии
при условии ![]() .
.
Функция Лагранжа:
![]() .
.
Условия стационарности:

Решение
системы: ![]() ,
, ![]() ,
, ![]() .
.
Исследуем выполнение условия достаточности, вычислив матрицу Гессе:
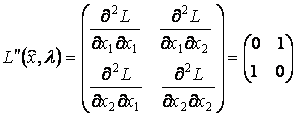 .
.
Второй
минор отрицателен, следовательно, условие достаточности не выполняется. Но этот
вывод сделан без учета того, что приращения аргументов не независимы, а
подчиняются уравнению связи
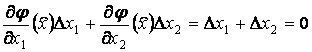 .
.
Вычислим
квадратичную форму с учетом того, что ![]() :
:
![]()
![]()
![]() .
.
Как видим, при ненулевых допустимых приращениях квадратичная форма всегда отрицательна. Значит, исследуемая точка есть точка максимума.
Пример 2. Найти экстремум функции ![]() при условии
при условии ![]() .
.
Действуем по той же схеме.
![]() .
.
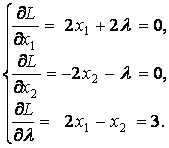
Решение
системы: ![]() ,
, ![]() ,
, ![]() .
.
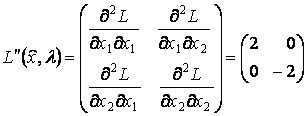 .
.
![]() ,
, 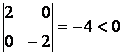 .
.
Второй минор отрицателен, следовательно, условие достаточности не выполняется. Проведем исследование знакоопределенности квадратичной формы с учетом уравнения связи. Из уравнения связи получаем:
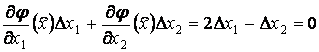
![]()
![]() .
.
Квадратичная форма:
![]()
![]() .
.
Из
соотношения ![]() следует, что
следует, что ![]()
![]() . Как видим, при ненулевых приращениях, удовлетворяющих
уравнению связи, квадратичная форма
всегда отрицательна. Значит, в стационарной точке максимум.
. Как видим, при ненулевых приращениях, удовлетворяющих
уравнению связи, квадратичная форма
всегда отрицательна. Значит, в стационарной точке максимум.
Пример 3.
(Неоклассическая модель потребления). Потребитель располагает суммой ![]() , которую тратит на приобретение различных товаров. Всего
имеется
, которую тратит на приобретение различных товаров. Всего
имеется ![]() товаров, цены которых
заданы вектором
товаров, цены которых
заданы вектором ![]() . Если обозначить спрос на товары вектором
. Если обозначить спрос на товары вектором ![]() , то задачу потребительского выбора можно сформулировать так:
, то задачу потребительского выбора можно сформулировать так:
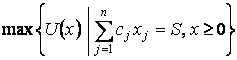 ,
,
где
![]() - функция полезности,
которая представляет собой меру удовлетворенности потребителя набором
- функция полезности,
которая представляет собой меру удовлетворенности потребителя набором ![]() . Согласно неоклассической теории
. Согласно неоклассической теории
![]() ,
,
где
![]() ,
, 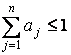 . В этом случае задача
принимает вид
. В этом случае задача
принимает вид
![]() ,
,
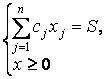
и является в силу свойств параметров целевой функции выпуклой. Заменим целевую функцию эквивалентной:
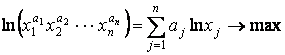 .
.
Приведем задачу к безусловному виду:
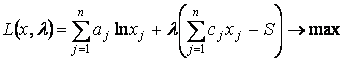 .
.
Условие стационарности:

Из первой
группы уравнений следует, что ![]() . Далее в результате простых выкладок получаем:
. Далее в результате простых выкладок получаем:
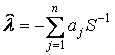 ,
, 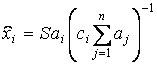 .
.
Матрица Гессе:
 .
.
Как видим, все нечетные миноры отрицательны, а четные положительны, следовательно, в стационарной точке находится максимум.