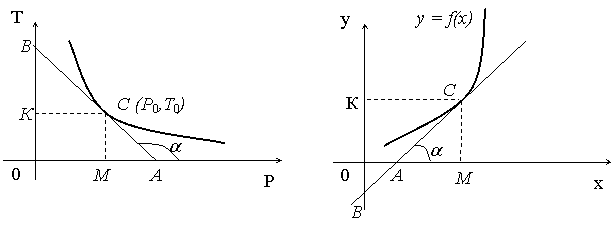Эластичность спроса

Введем новое для нас понятие эластичности функции . В отличие от производной, которая измеряет чувствительность функции к изменению аргумента и зависит от выбора единиц измерения, эластичность показывает, на сколько процентов изменяется при изменении на 1%.

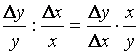Составим относительное изменение аргумента и относительное изменение функции . Найдем их отношение: . Предел этого отношения при называется эластичностью функции и обозначается :

,

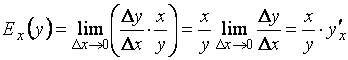т. е. эластичность функции есть производная этой функции по , умноженная на отношение значения аргумента к значению функции.

Найдем эластичность некоторых элементарных функций.

1. Эластичность степенной функции постоянна и равна показателю степени . Действительно, .

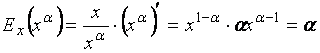2. Эластичность показательной функции пропорциональна аргументу .

В самом деле, .

3. Эластичность линейной функции :

.

4. Эластичность логарифмической функции :

.

Разобраться в геометрическом смысле эластичности удобно на примере функциональной зависимости спроса товара от его цены : .

Рис. 1		Рис. 2

Рис. 3

Так как функция спроса убывающая, то ее производная отрицательна, а значит, . Найдем эластичность этой функции в произвольной точке (рис. 1). Для этого проведем касательную к графику в точке и рассмотрим rАСМ и rСВК. Эти треугольники подобны, следовательно, . Но из rАСМ (по геометрическому смыслу производной).

Откуда 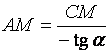и 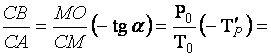- по определению есть эластичность функции спроса в точке . Знак "минус" показывает, что спрос уменьшается при увеличении цены.

Таким образом, , т.е. геометрически эластичность убывающей функции равна отношению расстояний по касательной от точки с координатами до точек ее пересечения с осями ординат и абсцисс, соответственно, взятому со знаком "-".

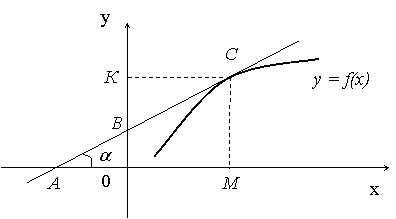
В случаях вогнутой и выпуклой возрастающих функций (соответственно, рис. 2 и рис. 3) эластичность по абсолютной величине также будет равна отношению , а знак эластичности будет определяться направлением отрезков и . Если точки и лежат по одну сторону от точки на касательной, как на рис. 2 и 3, то в формуле следует выбрать знак "+".

Если и лежат по разные стороны от точки , как на рис. 1, то в формуле нужно выбрать знак "-".

Отметим, что эластичность функции на рис. 2 больше единицы (так как ), а на рис. 3 меньше единицы (так как ).

Введем понятия эластичного , неэластичного и нейтрального спроса и исследуем динамику выручки при различных видах спроса.

Общие расходы населения на данный товар (выручка от его продажи) при цене составляют . Предельная выручка равна

или .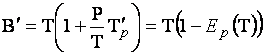

1) Если спрос эластичен, т.е. , то и с повышением цены выручка от продажи товара снижается.

2) При нейтральном спросе и выручка практически не зависит от цены. В этом случае и , т.е. при нейтральном спросе его размер обратно пропорционален цене ().

3) При неэластичном спросе () выручка увеличивается с ростом цены, так как в этом случае .

Из сказанного видно, что знание эластичности спроса на данный товар позволяет прогнозировать направление изменения суммы выручки под влиянием повышения или снижения цены.

Очевидно, что каждой фирме выгодно, чтобы спрос на ее продукцию был неэластичным, ибо в такой ситуации существует возможность назначать сравнительно высокие цены. Значит, фирма должна прилагать все усилия к поддержанию спроса на ее товар на достаточно высоком уровне. Достижению этой цели способствуют хорошее качество продукции, четко организованное обслуживание потребителей, высокое качество рекламы.

Пример. Известно, что эластичность спроса на товар составляет . Определите, как изменится доход от реализации товара, если цену на него увеличить на 5%.

Решение.

Так как эластичность показывает, на сколько процентов изменяется функция при изменении аргумента на 1%, то при эластичности увеличение цены на 1% вызывает уменьшение спроса на .

Увеличение цены на 5% способствует уменьшению спроса на 0,4% 5=2%. Цена выросла на 5% и стала равной 105%, или 1,05, где - старая цена. Если - спрос, соответствующий старой цене , то 0,98× - величина спроса при цене 1,05.

Выручка от реализации товара по цене составляла денежных единиц.

После увеличения цены выручка изменилась и стала равной

.

Последнее равенство означает, что выручка возросла приблизительно на 3% .

Таким образом, пример подтверждает, что при неэластичном спросе () увеличение цены приводит к возрастанию выручки.

Для функции нескольких переменных можно ввести по аналогии с эластичностью функции одной переменной понятие частной эластичности относительно переменной :

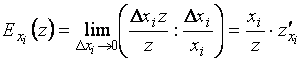, где - частное приращение функции по аргументу .

В производственной функции Кобба – Дугласа , выражающей результат производственной деятельности от обусловивших его факторов и , - величина произведенного общественного продукта, - затраты труда, - объем производственных фондов, - некоторые положительные постоянные.

Найдем для этой функции и :

,

.

Таким образом, показатели и приближенно показывают, на сколько процентов изменится выпуск продукции при изменении только затрат труда или только объема производственных фондов на 1%.