Отыскание наибольшего
и наименьшего значений функции,
непрерывной на отрезке
Согласно теореме Вейерштрасса функция, непрерывная
на отрезке, достигает на нем своих наибольшего и наименьшего значений
(глобального максимума и глобального минимума).
Они могут достигаться как на концах отрезка, так и в его внутренних
точках. В последнем случае это будут точки экстремума.
Отсюда получаем такой порядок
отыскания наибольшего и наименьшего
значений функции на отрезке.
1. Найти производную 
.
2. Найти критические точки
функции, т.е. точки, лежащие внутри отрезка, в которых 
или не существует.
3. Найти значения функции на
концах отрезка и в критических точках.
4. Из полученных чисел выбрать
наибольшее 
и наименьшее 
.
Пример 1. Найдите наибольшее и наименьшее значения функции 
на отрезке 
.
Решение.
1. Вычисляем 
.
2. Решаем уравнение 
(производная существует
на всем отрезке):
, 
, 
.
3. Вычисляем значения функции в критической точке 
и на концах отрезка,
т.е. в точках 
и 
: 
, 
, 
.
4. Сравнивая полученные числа,
заключаем, что 
, 
.
Ответ можно записать в виде 
, 
.
Замечание. Если функция 
непрерывна в интервале
или в полуинтервале,
то она может и не принимать на нем наибольшее и наименьшее значения.
Но имеет место сравнительно часто
встречающаяся ситуация, когда функция в
некотором интервале имеет единственный экстремум.
Справедливо следующие
утверждение. Если дифференцируемая
функция имеет в интервале единственную точку максимума (минимума), то
наибольшее (наименьшее) значение функции совпадает с максимумом (минимумом)
этой функции, а наименьшего (наибольшего) значения не существует.
Пример 2. Найдите наибольшее и наименьшее значения функции 
в интервале 
.
Решение.
Функция дифференцируема в
заданном интервале: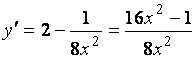 
.
Производная при 
, но критической точкой является лишь 
.
Находим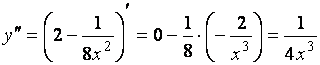 
и вычисляем 
.
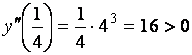По второму достаточному условию существования
экстремума функция имеет минимум в точке 
, равный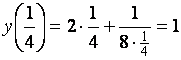 
.
Следовательно, 
, 
не существует.