Производная сложной и обратной функций

Пусть теперь задана сложная функция , т.е. переменная есть функция переменной , а переменная есть, в свою очередь, функция от независимой переменной .

Теорема. Если и - дифференцируемые функции своих аргументов, то сложная функция является дифференцируемой функцией и ее производная равна произведению производной данной функции по промежуточному аргументу и производной промежуточного аргумента по независимой переменной:

.

Утверждение легко получается из очевидного равенства (справедливого при и ) предельным переходом при (что в силу непрерывности дифференцируемой функции влечет ).

Перейдем к рассмотрению производной обратной функции.

Пусть на множестве дифференцируемая функция имеет множество значений и на множестве существует обратная функция .

Теорема. Если в точке производная , то производная обратной функции в точке существует и равна обратной величине производной данной функци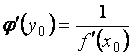и: , или

.

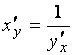Эта формула легко получается из геометрических соображений.

Так как есть тангенс угла наклона касательной линии к оси , то есть тангенс угла наклона той же касательной (той же линии ) в той же точке к оси .

Если и острые, то 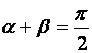, а если тупые, то .

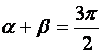В обоих случаях 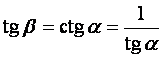. Этому равенству и равносильно равенство

.
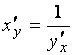