Основные теоремы

дифференциального исчисления

Приведем без доказательства теоремы известных французских математиков Ферма, Ролля и Лагранжа, сопроводив каждую из них геометрической иллюстрацией.

Теорема Ферма. Если дифференцируемая на промежутке функция достигает наибольшего или наименьшего значения на этом промежутке в его внутренней точке , то производная функции в этой точке равна нулю: .

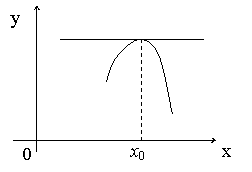Геометрически это означает, что в точке наибольшего или наименьшего значения, лежащей внутри промежутка , касательная к графику функции горизонтальна (параллельна оси абсцисс), ибо ее угловой коэффициент .

Теорема Ролля. Пусть функция удовлетворяет следующим условиям:

1) непрерывна на отрезке ;

2) дифференцируема в интервале ;

3) на концах отрезка принимает равные значения: .

Тогда в существует точка (по крайней мере, одна) такая, что производная в ней равна нулю: .

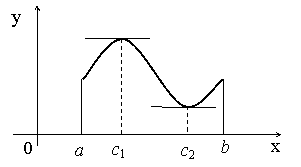
Геометрически это означает, что при выполнении условий теоремы в интервале найдется хотя бы одна точка, в которой касательная параллельна оси абсцисс.

Теорема Лагранжа. Пусть функция удовлетворяет следующим условиям:

1) непрерывна на отрезке [a, b];

2) дифференцируема в интервале .

Тогда в интервале существует точка (хотя бы одна), в которой производная равна отношению приращения функции к приращению аргумента на всем отрезке :

.

Заметим, что теорема Ролля является частным случаем теоремы Лагранжа, а доказательство теоремы Лагранжа сводится к применению теоремы Ролля к некоторой вспомогательной функции.

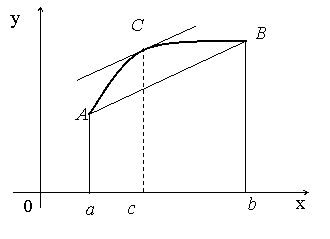Геометрический смысл теоремы заключается в том, что при выполнении ее условий на дуге графика найдется точка (хотя бы одна) с абсциссой такая, что касательная в ней к графику функции параллельна хорде : угловой коэффициент хорды , а угловой коэффициент касательной ; равенство же угловых коэффициентов двух прямых обеспечивает их параллельность.