Задача определения оптимальной

фондовооруженности труда

Предположим, что ,

где - затраты живого труда;

- затраты овеществленного труда;

- коэффициенты эластичности;

- коэффициент влияния неучтенных факторов.

Предположим, что известны параметры, необходимые для расчета балансовой прибыли:

- удельный фонд заработной платы;

- коэффициент, характеризующий норму затрат сырья на единицу товарной продукции;

- коэффициент амортизации;

- балансовая прибыль как разность между стоимостью товарной продукции и затратами;

- себестоимость,

тогда прибыль можно рассчитать как

.

Разделив обе части равенства на себестоимость, т.е.

,

получим рентабельность

.

Определим рентабельность как функцию фондовооруженности, т.е.. Для этого разделим числитель и знаменатель дроби

на

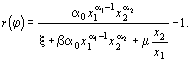
Если коэффициенты эластичности то

,

тогда

=.

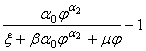Определим фондовооруженность, при которой рентабельность достигает своего максимального значения. Для этого найдем частную производную функции r(φ) по φ:

.

Экстремум функции достигается в точке, где производная либо не существует, либо равна нулю.

Знаменатель этой дроби всегда отличен от нуля. Следовательно, функция достигает экстремума, когда .

Первый сомножитель в ноль не обращается никогда, так как , поэтому для получения экстремума функции второй сомножитель должен быть равным нулю: .

Отсюда

.

Это точка, в которой рентабельность достигает своего экстремума.

Знак производной определяется знаком выражения . Это линейная функция относительно , причем убывающая, так как .

Отсюда следует, что при производная отрицательна, при - положительна.

Следовательно, при переходе через точку производная меняет свой знак с положительного на отрицательный, т.е. точка - точка максимума, и рентабельность достигает максимума при .