Функции спроса

Решение задачи потребительского выбора называется точкой спроса. Она зависит от цен и дохода I и является функцией цен и дохода, т.е. функцией спроса. С другой стороны, функция спроса представляет вектор-функцию вида

Таким образом, функция спроса представляет набор n функций, каждая из которых зависит от n + 1 аргумента:

…

Эти функции называются функциями спроса соответствующих товаров.

Пример 1. Для набора из двух товаров на рынке, известных ценах на них p₁, p₂, доходе I найти функции спроса, если функция полезности вида

Решение. Дифференцируя функцию полезности, получим

Подставляя выражения u^¢₁ и u^¢₂ в

,

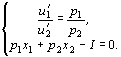получим систему

Из первого уравнения следует, что затраты денежных средств на оба товара должны быть одинаковыми, так как . Из второго уравнения получаем, что функции спроса

Таким образом, расход на каждый товар составляет половину дохода потребителя, а количество приобретенного товара равно затраченной на него сумме, поделенной на цену товара.

Модель потребительского спроса с функцией полезности мультипликативного вида

(1)

где a_i - минимально необходимое количество i-го товара.

Набор товаров можно рассматривать в качестве минимальной корзины потребления. Для приобретения минимального набора необходимо, чтобы доход был больше стоимости этого набора, т.е.

(2)

Показатели степеней a_i > 0 в (1) характеризуют относительную "ценность" соответствующих товаров для потребителя.

Добавив к функции (1) бюджетные ограничения, получим задачу потребительского выбора, которую называют моделью Р. Стоуна. Приравняв к нулю частные производные функции Лагранжа L по всем переменным, получим систему n + 1 уравнений:

Из соотношений получаем выражения для неизвестных x_i:

(3)

Умножим каждое из уравнений (3) на lp_i и просуммируем по i, получим

Отсюда отношение

будет иметь вид

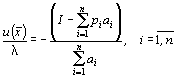(4)

Подставляя это выражение в (2), получим в окончательном виде формулы функций спроса:

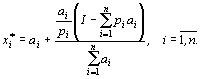
Рассмотрим частный случай модели Стоуна.

В этом случае из (4) получаем

т.е. доход I делится на n равных частей и количество приобретаемого i-го товара обратно пропорционально его цене. В этом случае спрос растет при росте дохода с единичной эластичностью и уменьшается с ростом цены с эластичностью, равной минус единице.