Кривые безразличия

В прикладных задачах и моделях потребительского выбора часто используется случай набора из двух товаров. В этом случае функция полезности зависит от двух переменных. При этом вводится понятие кривой безразличия, под которой понимается кривая, соединяющая потребительские наборы с одним и тем же уровнем удовлетворения потребностей индивида. Кривые безразличия представляют собой линии уровня функции или сечения поверхности плоскостями, параллельными плоскости Х₁О Х₂. Уравнение кривой безразличия:

. (1)

Множество кривых безразличия называется картой кривых безразличия и изображается на плоскости Х₁О Х₂ в виде семейства кривых.

В случае многомерной функции полезности, определенной в пространстве многомерных наборов, аналогично вводится понятие поверхности безразличия.

Рассмотрим основные свойства кривых безразличия.

1. Кривые безразличия, соответствующие разным уровням удовлетворения потребностей, не касаются и не пересекаются. Это следует из выражения (1).

2. Кривые безразличия убывают. Рассмотрим уравнение этой линии в виде

, (2)

которое можно получить из (1). Дифференциал функции вдоль линии уровня равен нулю, т.е.

откуда следует, что первая производная функции (2)

(3)

отрицательна по свойству 1 функции полезности.

3. Кривые безразличия выпуклы вниз. Действительно, вторая производная функции (2), согласно правилу дифференцирования частного, вычисляется:

.

Согласно свойствам 2 и 3 функции полезности, выражение в правой части этого равенства отрицательно и график функции (2) выпуклый вниз. Характерный вид кривых безразличия функции полезности приведен на рис. 1.

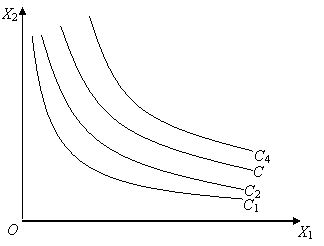
Рис. 1

Из выражения (3) можно получить следующее приближенное равенство:

которое показывает, на сколько индивид должен увеличить или уменьшить потребление второго продукта при уменьшении или увеличении потребления первого продукта на одну единицу, не изменяя уровня удовлетворения своих потребностей. Отношение называется нормой замены первого продукта вторым, а величина - предельной нормой замены первого продукта вторым.

Пример. Пусть первый товар имеет предельную полезность, равную 8, а второй товар - 4, тогда при уменьшении потребления второго товара на единицу нужно увеличить потребление первого товара на 2 единицы при том же уровне удовлетворения потребностей.