Транспортная задача

Постановка задачи и ее математическая модель

В m пунктах отправления (поставщики) имеется однородный груз в определенных количествах. Этот груз необходимо доставить в n пунктов назначения (потребители) в определенных количествах. Требуется составить план перевозок груза так, чтобы максимально удовлетворить всех потребителей, вывезти груз от поставщиков и чтобы общие затраты на перевозки были минимальными.

Введем обозначения.

i - номер пункта отправления , ;

j - номер пункта назначения, ;

b_i- наличие груза в i-м пункте отправления;

a_j -потребность в грузе j-го пункта назначения;

c_ij- стоимость перевозки единицы груза из i-го пункта отправления в j-й пункт назначения;

x_ij - количество груза, которое нужно перевезти из i-го пункта отправления в j-й пункт назначения.

Все данные располагают в таблице, которую называют распределительной таблицей:

Потребители Поставщики		1	2	…	n
		a1	a2	…	an
1	b1	c11 x11	c12 x12	…	c1n x1n
2	b2	c21 x21	c22 x22	…	c2n x2n
…	…	…	…	…	…
m	bm	cm1 xm1	cm2 xm2	…	cmn xmn

Определение 1. Если , то транспортная задача называется задачей закрытого типа, в противном случае, т.е. , - открытого типа.

Рассмотрим случай

.

Найдем затраты на перевозки груза.

с₁₁ х₁₁ - затраты на перевозку х₁₁ единиц груза из первого пункта отправления в первый пункт назначения.

с₁₂ х₁₂ - затраты на перевозку х₁₂ единиц груза из первого пункта отправления во второй пункт назначения и т.д.

Тогда общие затраты на транспортировку груза составят:

c₁₁x₁₁ + c₁₂x₁₂ +…+c_1nx_1n + c₂₁x₂₁ + c₂₂x₂₂ +…+c_2nx_2n +c_m1x_m1 +

+ c_m2x_m2 +…+c_mnx_mn =.

Целевая функция имеет вид

.

Составим ограничения по запасам груза. Из первого пункта отправления груз доставляется в пункты потребления соответственно в количествах х₁₁, х₁₂, …, х_1n, а всего можно вывезти b₁ единиц груза, следовательно, х₁₁ + х₁₂+…+ х_1n=b₁. Аналогично можно записать ограничения по остальным пунктам отправления. Получим систему уравнений

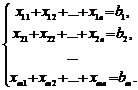
Ограничения по потребностям: в первый пункт потребления доставляют груз из пунктов отправления соответственно в количестве х₁₁ + х₁₂ +…+ х_m1, а потребность этого пункта равна а₁, получим уравнение х₁₁, х₁₂, …, х_m1=а₁.

Аналогично составляем ограничения по остальным пунктам назначения. Получим

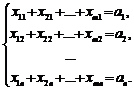
Так как х_ij - количество перевозимого груза, следовательно, х_ij³0.

Математическая модель закрытой транспортной задачи: найти наименьшее значение функции

при ограничениях:

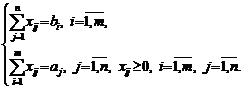
Система ограничений транспортной задачи состоит из m+n уравнений с m× n неизвестными.

Теорема 1. Ранг матрицы системы ограничений транспортной задачи на единицу меньше числа уравнений, т.е. r = m+n-1.

Теорема 2. Для того чтобы система ограничений транспортной задачи была совместной, необходимо и достаточно, чтобы выполнялось равенство

Доказательство.

Необходимость. Дано, что система ограничений транспортной задачи совместна. Пусть .

Подставим это решение в уравнения системы:

Просуммируем первое уравнение по i, а второе по j:

.

Левые части этих равенств равны, следовательно, равны и правые части, т.е.

.

Достаточность. Предположим, что

.

Возьмем числа

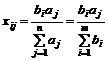
и покажем, что они удовлетворяют системе ограничений транспортной задачи. Для этого подставим эти числа в уравнения

и

Получим

,

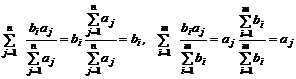и так как x_ij ³0, следовательно, совокупность чисел x_ij, взятых таким образом, является допустимым решением системы ограничений транспортной задачи.

Область допустимых решений транспортной задачи ограниченная, так как

.

Тогда на основании теоремы об экстремуме целевой функции можно утверждать, что транспортная задача с закрытой моделью имеет оптимальное решение, совпадающее хотя бы с одним из опорных решений.

Транспортную задачу можно решить симплексным методом, но существуют более простые методы решения транспортных задач, которые являются модификацией симплексного метода. В них применяется тот же прием последовательного улучшения решений, который состоит из трех этапов:

1) находится исходное опорное решение;

2) оценка решения на оптимальности;

3) переход к другому, лучшему опорному решению путем однократного замещения одной базисной переменной на свободную.

Нахождение исходного опорного решения

Транспортная задача задана в виде распределительной таблицы:

aj bi		1	2	…	n
		a1	a2	…	an
1	b1	c11	c12	…	c1n
2	b2	c21	c22	…	c2n
…	…	…	…	…	…
m	bm	cm1	cm2	…	cmn

Пусть . В каждой конкретной задаче математическая модель не составляется, а достаточно иметь распределительную таблицу. Процесс решения задачи также оформляется в таблицах.

Правило "северо-западного угла".

По правилу "северо-западного угла" начинают распределение поставок с северо-западной клетки. Берут .

Затем ,

затем и т.д.

Теорема 3. Решение, найденное по правилу "северо-западного угла", является опорным решением системы ограничений транспортной задачи.

Пример 1. Транспортная задача задана распределительной таблицей:

aj bi		1	2	3	4	5
		100	70	80	150	100
1	200	7	5	2	3	4
2	250	6	4	5	2	7
3	50	5	8	3	5	9

, , .

Найдем исходное опорное решение по правилу "северо-западного угла".

; ;

; ;

; ;

.

Нашли исходное опорное решение, которое записывается в таблицу:

aj bi		1	2	3	4	5
		100	70	80	150	100
1	200	7 100	5 70	2 30	3	4
2	250	6	4	5 50	2 150	7 50
3	50	5	8	3	5	9 50

Заполненные клетки в таблице соответствуют базисным переменным, а свободные клетки - свободным переменным. Число занятых клеток должно равняться рангу системы ограничений, т.е. r = m+n-1=3+8-1=7.

Найдем затраты на поставки груза по найденному плану:

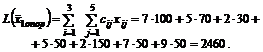
Нахождение опорного решения по правилу

"минимального элемента"

При нахождении исходного опорного решения по правилу "северо-западного угла" совершенно не учитываются затраты с_ij. По правилу "минимального элемента" в первую очередь заполняются клетки с наименьшим тарифом.

Найдем опорное решение в задаче по правилу "минимального элемента". Начинаем заполнять таблицу с клетки, имеющей наименьший тариф с₁₃=2.

Пусть

; ;

; ;

; ;

.

aj bi		1	2	3	4	5
		100	70	80	150	100
1	200	7	5	2 80	3 120	4
2	250	6 100	4 70	5	2 30	7 50
3	50	5	8	3	5	9 50

Найдем

<.

Замечание. При нахождении исходного опорного решения может оказаться, что число занятых клеток меньше ранга, т.е. решение вырожденное. В этом случае в свободные клетки ставят 0, чтобы число занятых клеток равнялось рангу, или находят опорное решение другим методом.

Критерий оптимальности решения транспортной задачи

Дана транспортная задача. Составим двойственную задачу, для этого каждому уравнению исходной задачи поставим в соответствие двойственные переменные:

,

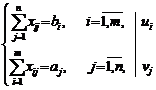
x_ij ³0, .

,

u_i + v_j £ c_ij , .

u_i , v_j свободны по знаку.

.

Пусть - оптимальное решение исходной задачи, тогда, по второй теореме двойственности, если x_ij >0, то соответствующее ему ограничение двойственной задачи выполняется как равенство u_i + v_j = c_ij , остальные ограничения выполняются как неравенство u_i + v_j < c_ij или u_i + v_j - c_ij<0.

Обозначим u_i + v_j - c_ij=D_ij и назовем оценкой свободной клетки. Получили критерий оптимальности решения транспортной задачи. Если u_i и v_j удовлетворяют условиям u_i + v_j = c_ij для занятых клеток и все оценки свободных клеток D_ij <0, то найденное решение оптимально.

Метод потенциалов

Переменные u_i и v_j являются оценками единицы груза b_i и a_j . Их называют потенциалами.

Метод потенциалов был предложен в 1949 г. Л.В. Канторовичем и М.К. Гавуриным.

Пусть транспортная задача имеет закрытую модель.

Алгоритм решения транспортной задачи

методом потенциалов

1. Найти исходное опорное решение.

2. Найти потенциалы из системы уравнений u_i + v_j = c_ij, справедливых для занятых клеток. Так как занятых клеток m+n-1, то система будет состоять из m+n-1 уравнений с m+n неизвестными. Эта система имеет бесконечное множество решений. Для того чтобы найти частное решение системы, придадим одному из неизвестных любое числовое значение, например u₁=0, и найдем значения остальных.

Потенциалы u_i и v_j записываем в столбце и в строке, которые добавляем к таблице.

3. Для всех свободных клеток найти оценки D_ij= u_i + v_j - c_ij.

4. Проверка решения на оптимальность.

Если все D_ij£0, то найденное решение оптимально.

Если среди оценок есть хотя бы одно положительное число, то найденное решение не оптимально и его надо улучшить.

5. Выбирается клетка с наибольшей положительной оценкой, и соответствующую переменную вводят в базис, для этого строят цикл для этой клетки. Даем поставку в эту клетку l. Тогда нарушится баланс и в строке, и в столбце, следовательно, нужно отнимать l от одной из поставок данного столбца и строки до тех пор, пока цикл не замкнется.

Свойства цикла:

1) в цикле всего одна свободная клетка, в которую пишем +l;

2) если строка или столбец участвует в цикле, то двумя клетками +l и -l;

3) число клеток цикла четно.

Можно доказать, что для любой свободной клетки можно построить единственный цикл.

6. Определяется l так, чтобы одна из занятых клеток освободилась и чтобы оставшиеся поставки x_ij ³0, т.е. l=min íx_ijý для четных клеток цикла.

7. Строится новая распределительная таблица, в которой изменяются только клетки цикла, остальные переписываются без изменения.

8. Переход в п. 2.

Пример 2. Возьмем пример 1, в котором исходное опорное решение найдено по методу "наименьшего тарифа", и оценим это решение на оптимальность.

aj bi		1	2	3	4	5	ui
		100	70	80	150	100
1	200	7	5	2 80	3 120-l	4 +l	u1=0
2	250	6 100	4 70	5	2 30+l	7 50-l	u2=-1
3	50	5	8	3	5	9 50	u3=1
vj		v1=7	v2=5	v3=2	v4=3	v5=8

u₁ + v₃ = 2, Получим 7 уравнений и 8 неизвестных.

u₁ + v₄ = 3, Если u₁ = 0, то v₃ = 2, v₄ = 3, u₂ = – 1, v₁ = 7, v₂ = 5, v₅ = 8, u₃ = 1

u₂ + v₁ = 6, Находим оценки свободных клеток по формуле D_ij = u_i + v_j – c_ij.:

u₂ + v₂ = 4, D₁₁=0+7-7=0, D₁₂=0+5-5=0, D₁₅=0+8-4= 4,

u₂ + v₄ = 2, D₂₃=-1+2-5=-4, D₃₁=1+7-5=3, D₃₂=1+5-8=-2,

u₂ + v₅ = 7, D₃₃=1+2-3=0, D₃₄=1+3-5=-1.

u₃ + v₅ = 9.

решение не оптимально, так как D₁₅=4>0 и D₃₁=3>0.

Построим цикл для клетки (1;5). В таблице в клетку (1;5) даем поставку = l, тогда нарушится баланс в первой строке и в пятом столбце. Это же количество поставок l вычтем из поставок клеток (1;4) и (2;5) и прибавим к (2;4)

Цикл построен.

120-l --------- +l

| |

| |

30+l ------ 50-l

Определим l=min í120;50ý=50.

Построим вторую таблицу, в которой изменятся только клетки цикла:

aj bi		1	2	3	4	5	ui
		100	70	80	150	100
1	200	7	5	2 80	3 70-l	4 50+l	u1=0
2	250	6 100-l	4 70	5	2 80+l	7	u2=-1
3	50	5 +l	8	3	5	9 50-l	u3=5
vj		v1=7	v2=5	v3=2	v4=3	v5=4

Составим систему уравнений и, полагая u₁=0, найдем значения всех остальных потенциалов:

u₁ + v₃ = 2, Þ v₃ = 2,

u₁ + v₄ = 3, Þ v₄ = 3,

u₁ + v₅ = 4, Þ v₅ = 4, Находим оценки свободных клеток:

u₂ + v₁ = 6, Þ v₁ = 7, D₁₁=0+7-7=0, D₁₂=0+5-5=0, D₂₃=-1+2-5= -4,

u₂ + v₂ = 4, Þ v₂ = 5, D₂₅=-1+4-7=-4, D₃₁=5+7-5=7, D₃₂=5+5-8=2,

u₂ + v₄ = 2, Þ u₂ =-1, D₃₃=5+2-3=4, D₃₄=5+3-5=3.

u₃ + v₅ = 9. Þ u₃ = 5.

Решение не оптимально, возьмем свободную клетку с наибольшей положительной оценкой D₃₁=7 и построим для нее цикл.

Определим l=min í100;70;50ý=50.

Строим третью таблицу:

aj bi		1	2	3	4	5	ui
		100	70	80	150	100
1	200	7	5	2 80	3 20	4 100	u1=0
2	250	6 50	4 70	5	2 130	7	u2=-1
3	50	5 50	8	3	5	9	u3=-2
vj		v1=7	v2=5	v3=2	v4=3	v5=4

Для определения потенциалов u₁ и v_j составим систему из семи уравнений с восемью неизвестными. Полагая u₁=0, найдем значения остальных потенциалов.

u₁ + v₃ = 2, Þ v₃ = 2,

u₁ + v₄ = 3, Þ v₄ = 3,

u₁ + v₅ = 4, Þ v₅ = 4, Находим оценки свободных клеток:

u₂ + v₁ = 6, Þ v₁ = 7, D₁₁=0+7-7=0, D₁₂=0+5-5=0, D₂₃=-1+2-5= -4,

u₂ + v₂ = 4, Þ v₂ = 5, D₂₅=-1+4-7=-4, D₃₂=-2+5-8=-5, D₃₃=-2+2-3=-3,

u₂ + v₄ = 2, Þ u₂ =-1, D₃₄=-2+3-5=-4, D₃₅=-2+4-9=-7.

u₃ + v₁ = 5. Þ u₃ = -2.

Так как все D_ij£0, следовательно, найденное решение оптимально, его можно записать в виде матрицы

Альтернативный оптимум в транспортных задачах

Если найденное решение оптимально, но среди оценок свободных клеток имеется хотя бы одна оценка, равная нулю, то задача имеет альтернативный оптимум. Чтобы найти второе оптимальное решение, нужно ввести в базис переменную, соответствующую свободной клетке с нулевой оценкой. Значение целевой функции при этом не изменится.

В предыдущей задаче D₁₁=0 и D₁₂=0, следовательно, задача имеет альтернативный оптимум. Возьмем клетку (1;1) и построим для нее цикл

+l -------- 20-l

| |

| |

50-l ------ 130+l

l=min í50;20ý=20.

Получим второе оптимальное решение:

.

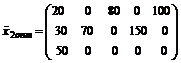Если взять клетку (1;2) и построить для нее цикл, то получим третье оптимальное решение:

+l -------- 20-l

| |

| |

70-l ------ 130+l

l=min í70;20ý=20.

.

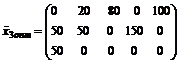Тогда

где

Открытая модель транспортной задачи

Если в транспортной задаче

,

то задача имеет открытую модель.

Если

,

то после распределения поставок все потребители будут удовлетворены, а у поставщиков остается часть груза в количестве

.

Следовательно, ограничения по потребителям не изменятся, а по поставщикам изменятся, а именно

Математическая модель задачи примет вид: найти наименьшее значение функции

при ограничениях:

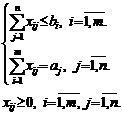
Если

,

то все потребители не могут быть удовлетворены. Ограниченные задачи примут вид

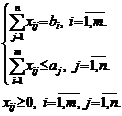
Открытая модель транспортной задачи имеет неканонический вид.

Приведем их к каноническому виду: найти наименьшее значение функции

при ограничениях:

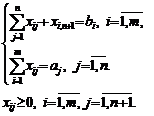
Найти наименьшее значение функции

при ограничениях:

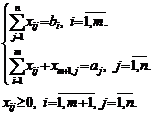
Балансовые переменные x_1,n+1, x_2,n+1, …, x_m,n+1 образуют дополнительный столбец в транспортной задаче, назовем его фиктивным потребителем, потребности которого

.

Балансовые переменные x _m+1,1, x _m+1,2, …, x _m+1,n образуют дополнительную строку в распределительной таблице, что будет соответствовать фиктивному поставщику, поставки которого

.

Таким образом, введя фиктивного поставщика или потребителя с нулевыми тарифами, получим закрытую модель.

Пример 3.

aj bi		1	2	3	4	5
		75	80	120	100	75
1	100	5	9	4	7	3
2	150	4	2	6	5	6
3	130	7	5	7	3	2

Так как

,

то введем фиктивного поставщика с нулевыми тарифами, запасы груза которого равны

.

Найдем исходное опорное решение методом минимального тарифа.

aj bi		1	2	3	4	5	ui
		75	80	120	100	75
1	100	5	9	4 100-l	7	3 +l	u1=0
2	150	4 25+l	2 80	6	5 45-l	6	u2=0
3	130	7	5	7	3 55+l	2 75-l	u3=-2
4	70	0 50-l	0	0 20+l	0	0	u4=-4
vj		v1=4	v2=2	v3=4	v4=5	v5=4

Оценим найденное решение на оптимальность, для этого по занятым клеткам таблицы подберем потенциалы:

u₁ + v₃ = 4,

u₂ + v₁ = 4, Если u₁=0, то v₃=4, v₄=-4, v₁=4, u₂=0, v₂=2,

u₂ + v₂ = 2, v₄=5, u₃=-2, v₅=4.

u₂ + v₄ = 5, Находим оценки свободных клеток:

u₃ + v₄ = 3, D₁₁=0+4-5=-1, D₁₂=0+2-9=-7, D₁₄=0+5-7=-2,

u₂ + v₅ = 2, D₁₅=0+4-3=1, D₂₃=0+4-6= -2, D₂₅=0+4-6= -2,

u₄ + v₁ = 0, D₃₁=-2+4-7=-5, D₃₂=-2+2-5=-5, D₃₃=-2+4-7=-5,

u₄ + v₃ = 0. D₄₂=-4+2-0=-2, D₄₄=-4+5-0=1, D₄₅=-4+4-0=0.

Найденное решение не оптимально, так как D₁₅>0 и D₄₄>0.

Построим цикл для клетки (1;5).

.

Построим вторую распределительную таблицу:

aj bi		1	2	3	4	5	ui
		75	80	120	100	75
1	100	5	9	4 55	7	3 45	u1=0
2	150	4 70	2 80	6	5	6	u2=0
3	130	7	5	7	3 100	2 30	u3=-1
4	70	0 5	0	0 65	0	0	u4=-4
vj		v1=4	v2=2	v3=4	v4=4	v5=3

Оценим второе решение на оптимальность.

Найдем потенциалы:

u₁ + v₃ = 4,

u₁ + v₅ = 3, Если u₁=0, то v₃=4, v₅=3, u₃=-1, v₄=4, u₄=-4,

u₂ + v₁ = 4, v₁=4, u₂=0, v₂=0.

u₂ + v₂ = 2, Находим оценки свободных клеток:

u₃ + v₄ = 3, D₁₁=0+4-5=-1, D₁₂=0+2-9=-7, D₁₄=0+4-7=-3,

u₃ + v₅ = 2, D₂₃=0+4-6= -2, D₂₄=0+4-5=-1, D₂₅=0+3-6= -3,

u₄ + v₁ = 0, D₃₁=-1+4-7=-4, D₃₂=-1+2-5=-4, D₃₃=-1+4-7=-4,

u₄ + v₃ = 0. D₄₂=-4+2-0=-2, D₄₄=-4+4-0=0, D₄₅=-4+3-0=-1.

Среди оценок нет положительных чисел, следовательно, найденное решение оптимально.

.
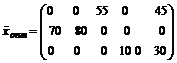