Правило составления двойственных задач в симметричном случае

 

1.      Каждому ограничению исходной задачи ставится в соответствие двойственная переменная y_i, где .

2.      Составляется целевая функция , коэффициентами которой будут свободные члены системы ограничений исходной задачи, а цель задачи меняется на противоположную:

.

3.      Составляется система ограничений двойственной задачи, при этом матрица из коэффициентов системы ограничений исходной задачи транспонируется, знак неравенства меняется на противоположный, свободными членами будут являться коэффициенты из целевой функции исходной задачи:

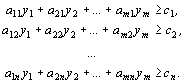
4.      Переменные y_i в двойственной задаче также неотрицательны, т.е.

.

Двойственная задача: найти наименьшее значение функции

при ограничениях:

.

 

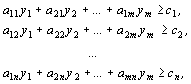
Правило составления двойственных задач в несимметричном случае

 

В несимметричном случае двойственная задача составляется по тем же правилам, что и в случае симметричной пары, но если двойственная переменная поставлена в соответствие ограничению уравнения, то эта переменная свободна по знаку, и обратно, если  то соответствующее ему ограничение двойственной задачи неравенство вида ³ , если задача решается на минимум, и £ , если на максимум.

Исходная задача задана в каноническом виде: найти наибольшее значение функции

при ограничениях:

.

Двойственная задача: найти наименьшее значение функции

при ограничениях:

,

где y_i свободны по знаку, .