Задачи с ограничениями, заданными

уравнениями. Метод множителей Лагранжа

Рассмотрим задачу нахождения экстремума функции при условии, что аргумент удовлетворяет системе уравнений

(1)

где - дважды непрерывно дифференцируемые скалярные функции векторного аргумента .

Уравнение связи (1) можно было бы использовать для того, чтобы в некоторой окрестности допустимой точки какие-либо
компонент вектора выразить через остальные :

. (2)

Это возможно, если в рассматриваемой точке существуют частные производные и определитель матрицы, составленной из значений частных производных, не равен нулю, т.е.

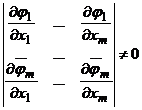. (3)

Если условие (3) выполняется, то, подставляя выражения для x_i из (2) в целевую функцию , мы придем к задаче на безусловный экстремум. Однако осуществить такой подход на практике чаще всего бывает трудно или даже невозможно. Поэтому используется другой подход - метод множителей Лагранжа. Он состоит в следующем:

1. Составляют функцию Лагранжа:

, (4)

где - вектор множителей Лагранжа.

2. Вычисляют и приравнивают к нулю частные производные функции Лагранжа:

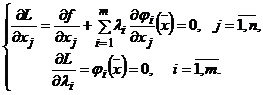
3. Решают систему уравнений, находят стационарную точку .

Анализ стационарной точки на наличие в ней экстремума в данном случае осуществляется более сложно, чем в случае безусловного экстремума. Поэтому при решении этого вопроса опираются на наглядные геометрические или содержательные, экономические соображения.

Пример. Найти стационарные точки функции

Решение. Составим функцию Лагранжа .

Выписываем условие стационарности:

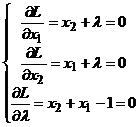
Решая данную систему, получим

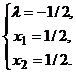
Таким образом, - стационарная точка.