Задача. Предприятие выпускает два вида изделий: А и В, используя для этого сырье трех видов, запасы n-го ограничены. Норма расхода сырья на изготовление единицы каждого вида изделий, а также прибыль, получаемая  от реализации изделий каждого вида следующие:

Сырье

Норма расхода сырья на единицу изделия (кг)

Запасы сырья (кг)

1

2

1

2

3

6

0

12

6

4

6

54

32

72

Прибыль от реализации единицы изделия в у.е.

4

2

 

 

Составить план выпуска изделий, дающий наибольшую прибыль предприятия. Составить математическую модель задачи, решить ее графически, составить двойственную задачу, решить ее и провести экономический анализ задачи.

 

Решение: Составим математическю модель. Пусть будет изготовлено х1 – изделий вида А и х2-изделий вида В. Тогда план производства представляется вектором (х1, х2).

Прибыль от реализации одного изделия вида А составляет 4 единицы, а от реализации х1 изделий – 4х1 единиц. Прибыль от реализации одного изделия вида В составляет 2 единицы, а от реализации х2 изделий – 2х2 единиц. Общая прибыль предприятия составит 4х1+2х2. Целевая функция задачи имеет вид:

На производство единицы изделия А расходуется 6 единиц сырья первого вида, а на х1 изделий А расходуется 6х1 единиц сырья первого вида. На производство единицы изделия В расходуется 6 единиц сырья первого вида, а на х2 изделий В расходуется 6х2 единиц сырья первого вида. Запасы сырья первого вида составляют 54 единицы , следователь 6х1+6х2£54. Аналогичные рассуждения проводятся по 2 и 3 видам сырья.  Количество произведенных изделий может быть либо положительным, либо равено нулю. Условий целочисленности на количество изделий не наложено. Математическая модель задачи имеет вид:

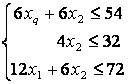
Решим задачу графическим методом. Область допустимых решений задачи -пересечение полуплоскостей, определенных каждым неравенством системы ограничений.

Для первого неравенство: 6х1+6х2£54 строим прямую 6х1+6х2=54. Взяв произвольную точку из одной из полуплоскостей, определим, является ли данная полуплоскость множеством решений данного неравенства. Например: точка 0 (0;0). 6×0+6×0£54 Þ0< 54, т.е. полуплоскость, содержащая т.0 является множеством решений неравенства 6х1+6х2£54.

Аналогично строим полуплоскости, определяемые остальными неравенствами.

                 Х2

 

             12

 

                 9  В                                 3

             А 8       D

 


         

                   

           

         

                 0               4  Е               9     1                             Х1           

                                     2    

 

 

 

 


Пересечение этих полуплоскостей образует область допустимых решений, т.е. многоугольник ОАВDЕ. По теореме об экстремуме целевой функции, если оптимальное решение существует, то оно совпадает с угловой точкой области допустимых решений. Для нахождения оптимального решения строим вектор  , перпендикулярно ему проводим линию уровня, которую перемещаем по направлению вектора , т.к. задача решается на max. Последняя точка пересечения линии уровня и области допустимых решений является оптимальным решением задачи. Если оптимальное решение совпадает с двумя угловыми точками области допустимых решений, например, х1 и х2, то любая точка отрезка [ х1, х2] является оптимальным решением, т.е.

 где                

 в т.D, которая лежит на пересечении I и П граничных прямых

                                                   

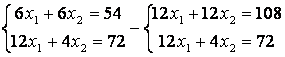
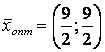
Составим двойственную задачу к исходной. В исходной задаче ограничения заданы неравенствами и на переменные наложено ограничение неотрицательности, то получим симметричную пару задач.

Каждому ограничению исходной задачи соответствует переменная в двойственной. Цель задачи меняется на противоположную. Транспонируется матрица коэффициентов задачи, коэффициенты при переменных в целевой функции заменяются сводными членами системы ограничений исходной задачи.

                             

                                 

                                                              

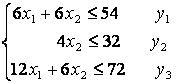
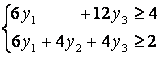
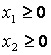
Исходя из теорем двойственности, найдем решение двойственной задачи.

т.е. >0, поэтому соответствующие им 1 и 2 ограничения двойственной задачи выполняются как равенства. Первое и третье ограничения исходной задачи выполняются как строка равенства Þ соответствующие им у1 и у3 положительны, а у2 =0.

Получили:

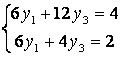
                                8у3=2,   

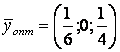
Экономический анализ. Для получения максимальной прибыли в ед. необходимо произвести  изделий вида А и - вида В, при этом сырье 1 и 3 видов будет израсходовано полностью и каждая дополнительно привлеченная единица сырья 1 вида принесет дополнительно ед. прибыли, а каждая дополнительно привлеченная единица сырья 3 вида даст дополнительно ед. прибыли. Сырье второго вида не используется полностью, и предприятие можно бы не покупать  ед. этого сырья.