Теория двойственности

Пример 1. Составить двойственную задачу к следующей: найти наибольшее значение функции

при ограничениях:

х₁ ³ 0, х₂ ³ 0, х₃ и х₄ свободны по знаку.

Двойственная задача: найти наименьшее значение функции

при ограничениях:

y₁, y₂ свободны по знаку, у₃ ³ 0, у₄ ³ 0.

Пример 2. Дана задача линейного программирования в неканоническом виде

,

х₁ ³ 0 , х₂ ³ 0.

Данная задача имеет оптимальное решение

Составим двойственную задачу:

у_i ³ 0, .

Из первой теоремы двойственности следует, что .

Применим вторую теорему двойственности: так как в оптимальном решении исходной задачи и , то на оптимальном решении двойственной задачи первое и второе ограничения двойственной задачи выполняются как равенства

Подставим в ограничения исходной задачи и получим, что третье ограничение выполняется как строгое неравенство:

9 × 23,53 + 4 × 21,18 = 296,49, т.е. 296,49<360 Þ у₃ = 0.

Получим систему трех уравнений с тремя неизвестными:

Решая систему, получим .

Пример 3. Найти наименьшее значение функции

при ограничениях:

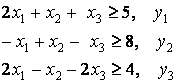
х_i ³ 0, .

Решение. Составим двойственную задачу:

,

у_i ³ 0,

Решим двойственную задачу симплексным методом, для этого приведем ее к каноническому виду

2у₁ - у₂ +2у₃+ у₄ =2,

у₁ + у₂ - у₃ + у₅ =1,

у₁ - у₂ - 2у₃ + у₆ =2,

.

Целевая функция остается без изменения.

сj	Б.п.	5	8	4		0	0	0	bi
		у1	у2	у3	у4		у5	у6
0 0 0	у4 у5 у6	2 1 1	-1 1 -1	2 -1 -2		1 0 0	0 1 0	0 0 1	2 1 3
Dj		-5	-8	-4		0	0	0	0
0 8 0	у4 у2 у6	3 1 2	0 1 0	1 -1 -3		1 0 0	1 1 1	0 0 1	3 1 4
Dj		3	0	-12		0	8	0	8
4 8 0	у3 у2 у6	3 4 11	0 1 0	1 0 0		1 1 3	1 2 4	0 0 1	3 4 13
Dj		39	0	0		12	20	0	44

.

Отбрасывая балансовые переменные, получим оптимальное решение двойственной задачи: .

Тогда по первой теореме двойственности .

Установим связь между балансовыми переменными двойственной задачи и основными переменными исходной задачи:

х₁®у₄, х₂®у₅, х₃®у₆.

Тогда х₁=D₄, х₂=D₅, х₃=D₆, .

Пример 4. Найти наибольшее значение функции

при ограничениях:

х_i ³ 0, .

Данная задача имеет оптимальное решение

.

Составим двойственную задачу: найти наименьшее значение функции

при ограничениях:

у₁ и у₂ свободны по знаку.

По первой теореме двойственности .

По второй теореме двойственности, так как в оптимальном решении исходной задачи х₂¹0 и х₃¹0, то, выписывая второе и третье ограничения двойственной задачи как уравнения, получим систему из двух уравнений с двумя неизвестными:

Решая эту систему, получим у₁= -2 и у₂=13, = (-2; 13).

Пример 5. Рассмотрим задачу определения плана выпуска продукции, дающего наибольшую прибыль

,

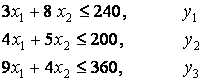
х₁ ³ 0, х₂ ³ 0.

Составим двойственную задачу:

,

.

Найдем решения обеих задач:

.

В оптимальном решении двойственной задачи , следовательно, третий вид сырья недефицитный, т.е. при расходуется не полностью. у₁>0 и у₂>0, следовательно, первое и второе сырье дефицитное, и поскольку у₂> у_1, второе сырье оказывает большее влияние на прибыль, есть смысл увеличивать в первую очередь запасы второго сырья.