Задача на условный экстремум.

Метод множителей Лагранжа

Пример 1. Найти экстремум функции при условии .

Решение. Из уравнения связи выразим х₂ через х₁ и подставим полученное выражение в функцию y:

Эта функция имеет единственный экстремум (минимум) при х₁ = 2. Соответственно, . Таким образом, точкой условного экстремума (минимума) заданной функции является точка ; = 0.

Пример 2. Найти экстремумы функции при условии

.

Решение. Заметим, что функции

и

непрерывны и имеют непрерывные частные производные.

Составим функцию Лагранжа:

.

Найдем частные производные и приравняем их к нулю.

.

Получаем две стационарные точки:

1) при ;

2) при .

Принимая во внимание характер целевой функции, линиями уровня которой являются плоскости, и функции (эллипс) заключаем, что в точке функция принимает минимальное значение, а в точке максимальное.

Пример 3. В области решений системы

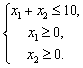
найти максимальное и минимальное значение функции при условии

Решение. Пересечением области допустимых решений и прямой является отрезок MN: M(0,6), N(6,0). Поэтому экстремальные значения функция может принимать либо в стационарных точках, либо в точках M и N. Для нахождения стационарной точки применим метод Лагранжа. Составим функцию Лагранжа

.

Найдем частные производные функции Лагранжа и приравняем их к нулю

Решая систему, получаем стационарную точку К(2,2;3,8). Сравним значения целевой функции в точках К, M, N:

y(K) = 4,76, y(N) = 77, y(M) = 29.

Следовательно, , ; , .