Совместность однородной системы

Рассмотрим однородную систему

.

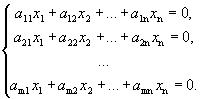Однородная система всегда совместна, так как всегда имеет тривиальное (нулевое) решение . Выясним, когда данная система имеет нетривиальное решение.

Теорема 1. Однородная система имеет нетривиальное решение тогда и только тогда, когда ранг матрицы, составленной из коэффициентов при неизвестных, меньше числа неизвестных.

Доказательство. Пусть система совместна. Это может быть тогда и только тогда, когда найдутся числа с₁, с₂, …, с_n, при подстановке которых в систему мы получим m тождеств. Эти m тождеств можно записать в виде

.

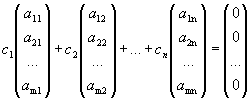Следовательно, система векторов-столбцов матрицы А линейно зависима. А это может быть тогда и только тогда, когда ранг системы векторов-столбцов меньше n, т.е. r(A)<n.

Следствие. Квадратная однородная система имеет нетривиальное решение тогда и только тогда, когда определитель матрицы, составленной из коэффициентов при неизвестных, равен нулю.

Доказательство. Так как r(A)<n, то столбцы матрицы линейно зависимы и, следовательно, определитель матрицы равен нулю.