Собственные векторы и значения матриц

Определение. Число называется собственным значением квадратной матрицы А, если найдется вектор такой, что А·=·. Вектор называется собственным вектором матрицы А, соответствующим данному собственному значению.

Теорема 1. Собственные значения матрицы А являются решениями уравнения

.

Это уравнение называется характеристическим уравнением матрицы А.

Теорема 2. Число различных собственных значений квадратной матрицы не превосходит ее порядка. Собственные векторы, отвечающие различным собственным значениям, линейно независимы.

Пример. Пусть дана матрица .

Составим и решим характеристическое уравнение.

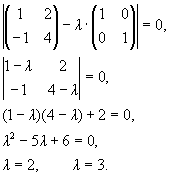
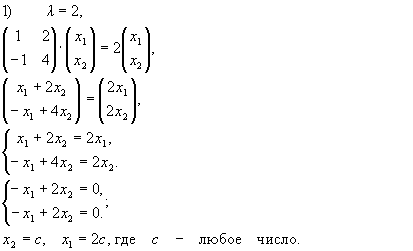
Вектор (2с,с) будет являться собственным вектором, соответствующим собственному значению 2.

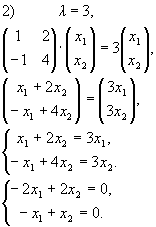
Вектор (с,с) будет являться собственным вектором, соответствующим собственному значению 3.

Векторы (2с,с) и (с,с) линейно независимы. Так как они двухмерные, то они образуют базис пространства Е².