Обратная матрица

Определение 1. Квадратная матрица называется вырожденной, если ее определитель равен нулю, и невырожденной - в противном случае.

Определение 2. Матрица А^-1 называется обратной к квадратной матрице А n-го порядка, если А·А^-1= А^-1·А=Е.

Теорема 1. Для любой невырожденной квадратной матрицы существует единственная обратная матрица.

Доказательство. 1 часть (единственность).

Предположим, что обратная матрица существует. Докажем, что она единственная. Предположим противное, т.е. существует две обратные матрицы: А^-1 и .

Тогда А·А^-1=А^-1·А=Е и А·=·А=Е.

Рассмотрим равенство

А·А^-1=Е.

Умножим его слева на .

·А·А^-1=·Е,

Е·А^-1=,

А^-1=.

Получили противоречие.

2 часть (существование). Дана матрица

А = , .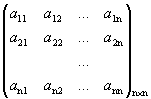

Построим обратную матрицу. Для этого совершим ряд действий:

1) заменим все элементы матрицы их алгебраическими дополнениями:

А*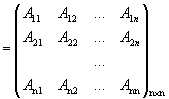 - матрица, присоединенная к матрице А;

2) транспонируем полученную матрицу:

(А*)^Т=;

3) разделим все элементы на число ½А½

.

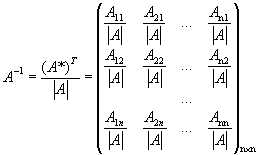Проверим, будет ли полученная матрица обратной к исходной. Для этого умножим матрицу А на А^-1. Элемент, стоящий в i-й строке и j-м столбце матрицы произведения, будет равен

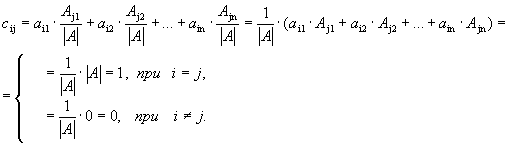
Элементы матрицы-результата совпадают с элементами единичной матрицы Е. Следовательно, А · А^-1=Е, т.е. А^-1 - обратная матрица к А.