Первообразная.
Неопределенный интеграл
Определение 1. Первообразной
функцией F(x) для функции f(x) называется функция, производная которой равна исходной функции.
(F(x))' = f(x).
Теорема 1 (теорема Коши). Любая непрерывная
на некотором множестве функция имеет на этом множестве первообразную.
Пример 9.1. Функция F(x) = x3 является первообразной функции f(x) = 3x2 так как
(x3)' = 3x2. Функции F1(x) = x3 +
3 и F2(x)
= x3 – 2 также являются первообразными функции f(x).
Любая функция вида F(x) = x3 + с, где с — произвольное число, является первообразной функции f(x).
Каждая функция может иметь
бесконечно много первообразных, которые отличаются на постоянное слагаемое.
Верно и обратное утверждение.
Теорема 2. Если F1(x) и F2(x) — две первообразные для функции f(x),
то они отличаются на постоянное слагаемое.
Доказательство. Рассмотрим функцию
Ф(х)
= F1(x) – F2(x).
Ф'(х)
= F1'(x)
– F2'(x)
= f(x) – f(x) = 0,
Ф(х)
= C,
F1(x)
= F2(x)
+ C.
Определение 2. Совокупность всех первообразных
данной непрерывной функции называется неопределенным интегралом от этой функции
и обозначается 
, где f(x)
именуется подинтегральной
функцией, выражение f(x)dx
— подинтегральным выражением.
Если F(x)
— некоторая первообразная данной функции, то = F(x) + C, где C — произвольная постоянная.
Процесс нахождения
неопределенного интеграла называется интегрированием данной функции, или
взятием интеграла от данной функции.
Первообразные имеют
следующий геометрический смысл.
Пусть F1(x) и F2(x) — первообразные функции y = f(x). Найдем их производные в точке х0.
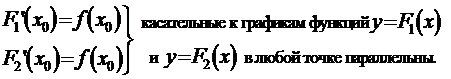
Следовательно,
и сами графики будут располагаться параллельно
(рис. 1).
На основании теоремы
9.2 F1(x) и F2(x) отличаются на постоянное слагаемое,
следовательно, один график можно получить из другого сдвигом на C единиц вдоль оси ОY.
F1(x) = F2(x) +
C.
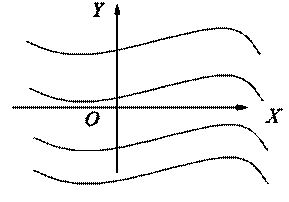
Рис. 1
Функция имеет бесконечно
много первообразных, которые отличаются друг от друга на постоянное слагаемое.
Графики всех первообразных представляют собой бесконечное семейство
параллельных кривых.