Интегрирование по частям и метод замены

переменной в определенном интеграле

1. Пусть функции u(x) и (x) имеют непрерывные производные на отрезке [a,b]. Проинтегрируем равенство для дифференциалов по отрезку [a,b].

,

,

,

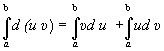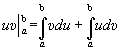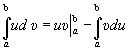- формула интегрирования по частям в определенном интеграле. Эта формула применяется к тем же типам интегралов, которые были рассмотрены в неопределенном интеграле.

2. Пусть y =f(x) непрерывна на отрезке [a,b] и на этом отрезке она имеет первообразную F(x).

.

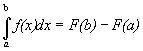Пусть функция y = (t) является дифференцируемой функцией на [] и ее производная непрерывна на []. Она переводит отрезок [] в [a,b].

: [] [a,b].

(a) = a, (b) = b (концы переводит в концы).

Тогда справедлива формула замены переменной в определенном интеграле:

.

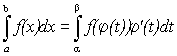Доказательство. ,

.

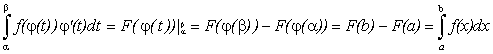Пример 1.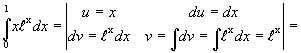

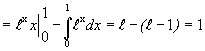
Пример 2. =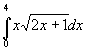

=.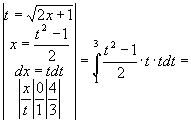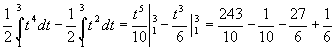