Свойства
определенного интеграла
Справедливы следующие
свойства определенного интеграла.
1. 
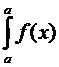dx 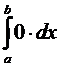= 0, 
= 0.
2. 
= – 
.
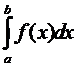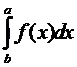3. Если функция y = f(x) интегрируема по большему из промежутков [a,b], [a,с], [с,b], то она интегрируема по двум другим
промежуткам, причем выполняется равенство
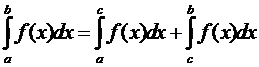
независимо от расположения точек а, b, c (рис. 1).
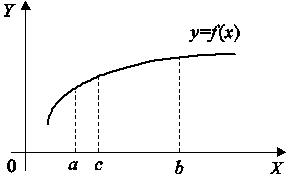
Рис. 1
Доказательство. 1. Случай a<c<b. Возьмем произвольное разбиение
отрезка [a,b]:
x0 = a < x1 < x2 <...< с <… < xn = b.
Очевидно, что для интегральных
сумм будет выполняться следующее равенство:
.
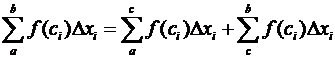Переходя к пределу при
измельчении длин отрезков разбиения, получим требуемое равенство.
2. Случай с < а < b. Согласно случаю 1
.
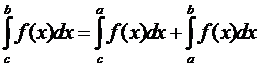Используя свойство 2, получим
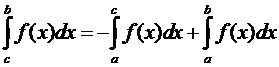, отсюда
.
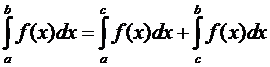Аналогично рассматриваются
остальные случаи.
4. Постоянный множитель
можно выносить за знак определенного интеграла.
.
.
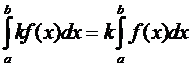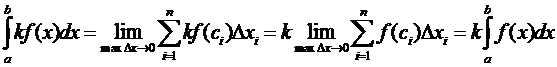5.
Если функции f(x) и g(x) интегрируемы по отрезку [a,b], то и их алгебраическая сумма также
интегрируема по [a,b], причем
интеграл от алгебраической суммы равен алгебраической сумме интегралов.
.
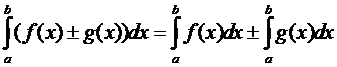Это равенство непосредственно следует
из равенства для интегральных сумм.
.
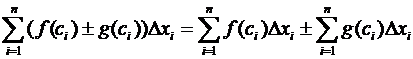6. Пусть функция y = f(x) определена на отрезке [a,b]. Рассмотрим функцию
Ф(х) =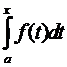 
.
Значение функции Ф(х)
в точке x2 равно площади
криволинейной трапеции, заключенной между графиком функции и осью ОХ на отрезке [a, x2] (рис. 2).
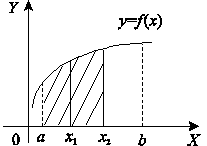
Рис. 2
В каждой точке
непрерывности функции f(x) функция Ф(х) имеет производную, которая равна f(x).
Ф' (х)
= f(x),
т. е. Ф(х) является первообразной
для функции f(x).