Геометрический смысл производной
 Определение 1. Касательной к плоской
кривой называется предельное положение секущей, когда вторая точка пересечения
неограниченно приближается по кривой к первой точке.
Определение 1. Касательной к плоской
кривой называется предельное положение секущей, когда вторая точка пересечения
неограниченно приближается по кривой к первой точке.
Пусть функция у=f(x)
определена и непрерывна на (a,b), ![]() . Дадим приращение аргументу
Dх
так, что точка х0+Dх
. Дадим приращение аргументу
Dх
так, что точка х0+Dх![]() . Функция получит приращение Dу=f(x0+Dx)-f(x0).
. Функция получит приращение Dу=f(x0+Dx)-f(x0).
Проведем секущую к графику через точки А(х0 , f(x0)), В(x0+Dx, f(x0+Dx)).
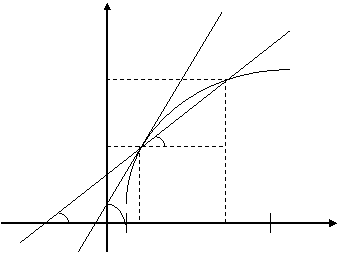 Y
Y
f(x0+Dx) B
y=f(x)
Dy
f(x0) A a C
a j Dx
a x0 x0+Dx b X
Рассмотрим DABC. ![]() ,
, ![]() .
.
При
![]()
![]() ,
,
секущая стремится к
касательной,
![]() ,
,
![]() ,
,
![]() .
.
Переходя к пределу при ![]() в равенстве
в равенстве ![]() , получим
, получим
![]() .
.
Производная
функции в точке равна тангенсу угла наклона касательной, проведенной к
графику функции в данной точке.