Эластичность функции, ее свойства

Определение 1. Коэффициентом эластичности функции y = f (x) в точке x₀ называется предел отношения относительного приращения функции к относительному приращению аргумента, когда приращение аргумента стремится к нулю ∆x → 0:

.

Из определения эластичности следует, что при малых значениях ∆x будет выполняться приближенное равенство:

.

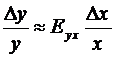т.е. коэффициент эластичность функции является коэффициентом пропорциональности между относительными изменениями величин y и x, он показывает приближенно, на сколько процентов изменится функция y = f (x) при изменении независимой переменной х на 1%.

Выразим коэффициент эластичности через производную функции.

,

.

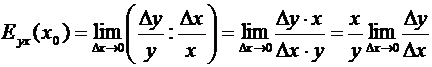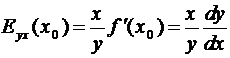Следовательно, чтобы существовал коэффициент эластичности в данной точке необходимо и достаточно чтобы существовала производная в этой точке.

Используя логарифмическое дифференцирование, получим:

.

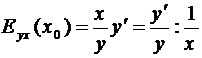
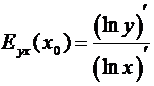Коэффициент эластичности совпадает с отношением логарифмических производных.

Геометрический смысл эластичности

По свойству  эластичности 

,

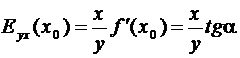где α - угол наклона касательной к графику функции y = f (x) в точке С(x₀, y₀ ).

Рассмотрим случай убывающей функции (рис. 1).

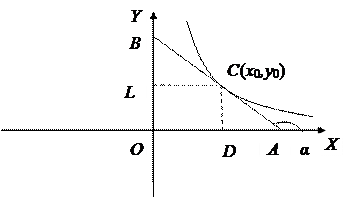
Рис. 1

Из ΔВCL: .

, .

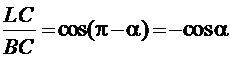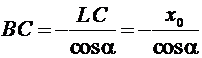Из ΔACD: .

, .

.

.

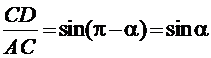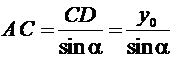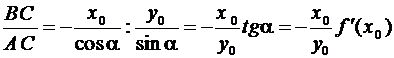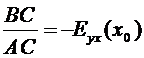Эластичность убывающей функции в точке равна отношению расстояний по касательной от точки С с координатами (x₀, y₀) до ее пересечения с осями ординат и абсцисс, взятому со знаком минус.

Рассмотрим случай возрастающей функции (рис. 2).

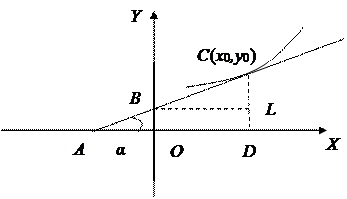
Рис. 2

Из ΔВCL: .

, .

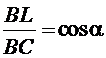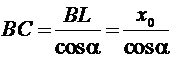Из ΔACD: .

, .

.

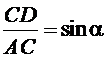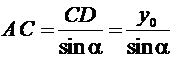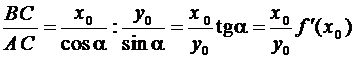
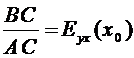Эластичность возрастающей функции в точке равна отношению расстояний по касательной от точки С с координатами (x₀, y₀) до ее пересечения с осями ординат и абсцисс, взятому со знаком плюс.

Свойства эластичности

Функция в зависимости от величины своей эластичности может быть:

Совершенно эластичная
Эластичная
Неэластичная
Совершенно неэластичная

Теорема 1. Эластичность является безразмерной величиной, т.е. не зависит от выбора единиц измерения величин y и x.

.

Доказательство.

.

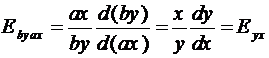Теорема 2. Коэффициенты эластичности взаимно обратных функций есть взаимно обратные величины.

Доказательство.

.

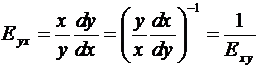Теорема 3. Эластичность произведения функций равна сумме эластичностей этих функций.

Доказательство. Пусть функции u и v дифференцируемы.

.

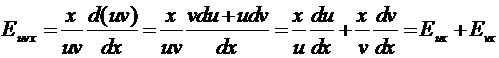Теорема 4. Эластичность частного функций равна разности эластичностей этих функций.

Доказательство. Пусть функции u и v дифференцируемы и v ≠ 0.

.

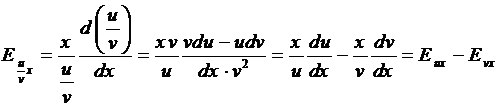Теорема 5. Эластичность суммы функций равна сумме эластичностей этих функций с весовыми коэффициентами.

Доказательство. Пусть функции u и v дифференцируемы.

.

.

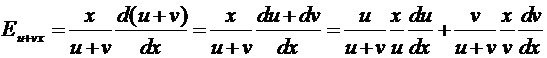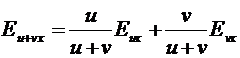Теорема 6. Для функций y = f (x) и x = g (t) эластичность y по t в точке t₀ удовлетворяет равенству:

.

Пример 1. Найти эластичность функций y = x^a.

.
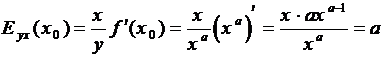