Асимптоты графика функции

Графики некоторых функции расположены на плоскости так, что они неограниченно приближаются к некоторой прямой. Эти прямые называются асимптотами к графику функции.

Определение 1. Прямая х=а называется вертикальной асимптотой к графику функции y=f(x), если хотя бы один из односторонних пределов , равен +¥ или -¥.

Как правило, в точке а функция терпит разрыв второго рода.

Определение 2. Прямая у=b называется горизонтальной асимптотой к графику функции y=f(x), если .

Определение 3. Прямая у=kx+b называется наклонной асимптотой к графику функции y=f(x), если функцию можно представить в виде f(x)=kx+b+, где - б.м. при .

Найдем параметры наклонной асимптоты.

1. Найдем k.

f(x)=kx+b+.

Разделим обе части равенства на х.

.

Переходя к пределу при , получим

,

.

2. Найдем b.

f(x)=kx+b+,

b+= f(x)-kx.

Переходя к пределу при , получим

.

Если k=0 и b¹0, то наклонная асимптота становится горизонтальной.

Пример. .

,

,

х=1 – вертикальная асимптота.

,

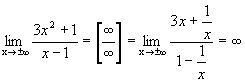горизонтальной асимптоты нет.

k=,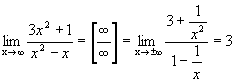

b=,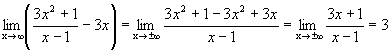

y=3x+3 – наклонная асимптота.

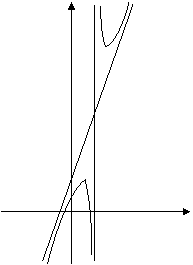Y

X