Экстремумы функции
Пусть функция y=f(x)
определена на интервале (a,b).
Определение 1. Точка х0Î(a,b)
называется точкой локального максимума (минимума) функции, если найдется
некоторая окрестность этой точки, для всех точек
которой будет выполняться условие:
![]() (
(![]() ).
).
Точки локального максимума и минимума называют
точками экстремума.
Теорема 1 (необходимый признак экстремума функции). Если точка х0 является точкой локального
максимума (минимума) функции, то производная
в этой точке равна нулю или не существует.
Доказательство. Пусть функция y=f(x) дифференцируема
на (a,b), ![]() найдется
число d такое, что:
найдется
число d такое, что:
"![]()
![]() .
.
Дадим аргументу приращение
Dx>0 так, что ![]()
![]() .
.
Переходя к пределу при ![]() , получим
, получим
![]() .
.
Дадим аргументу приращение Dx<0 так, что
![]()
![]() .
.
Переходя к пределу при ![]() , получим
, получим
![]() .
.
Эти
неравенства выполняются одновременно только в двух случаях:
а)
![]() ,
,
b) ![]() не существует.
не существует.
Следствие. В точке экстремума касательная:
a) либо параллельна оси ОХ,
b) либо не существует.
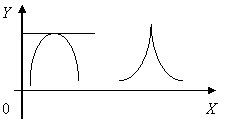
Данный признак не является достаточным для существования экстремума, т.е. из того, что производная равна нулю или не существует в некоторой точке, не следует, что в этой точке есть экстремум.
 Y Y
Y Y
0 X 0 X
y=x3 y=![]()
Точки, в которых первая
производная равна нулю или не существует, называют критическими точками первой
производной. Если функция имеет экстремумы, то они могут быть только в
критических точках.
Пусть функция y=f(x)
определена и непрерывна в некоторой окрестности точки х0 и дифференцируема в этой окрестности (за исключением,
быть может, точки х0).
Теорема 2 (достаточный признак
экстремума). Если
первая производная функции в точке х0
равна нулю или не существует и при переходе через нее производная меняет знак,
то данная точка является точкой экстремума, причем если знак меняется с ''+''
на ''-'', то это точка максимума, с ''-'' на ''+'' – точка минимума.
Доказательство.
Пусть в
точке х0 производная дифференцируемой функции равна нулю или не существует и при переходе
через нее производная меняет знак с
''+'' на ''-''.
![]()
![]()
![]() возрастает на
возрастает на ![]()
![]()
![]()
![]() убывает на
убывает на
![]()
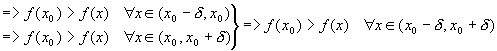 .
.
Следовательно, х0 - точка
максимума. Случай минимума рассматривается аналогично.