Точки разрыва
функции
Функция
является непрерывной в точке, если
.
Определение 1. Точки, в которых нарушается условие
непрерывности, называют точками разрыва функции.
Определение 2. Точка разрыва х0
называется точкой разрыва первого рода, если существуют конечные односторонние пределы в этой точке.
Определение 3. Точка разрыва первого рода
называется точкой устранимого разрыва, если односторонние пределы в этой точке
равны.
Определение 4. Скачком функции в точке разрыва
первого рода называется модуль разности односторонних пределов в этой точке.
Определение
5. Точка х0
называется точкой разрыва второго рода, если она не является точкой разрыва
первого рода (если хотя бы один из односторонних пределов не существует или
равен + ¥(–¥)).
Пример 1.Исследуем
функцию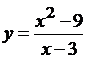 
в точке х
= 3.
,
.
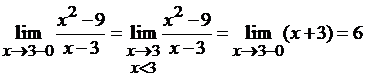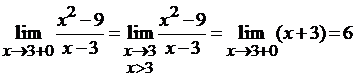Следовательно, х = 3 — точка устранимого разрыва (рис.
1).
Рис. 1
Функцию можно доопределить до
непрерывной функции:
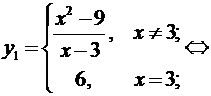y = x + 3 — непрерывная функция.
Пример 2. y = [x] — целая
часть числа.
Рассмотрим точку х = 1.
,
.
Следовательно, х = 1 —
точка разрыва первого рода, скачок в ней равен единице (рис. 2).
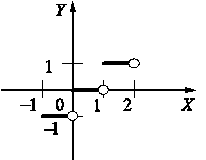
Рис. 2
Пример 3. Рассмотрим
функцию 
в точке х
= 0.
,
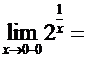
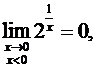
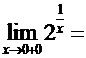
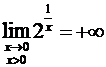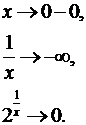
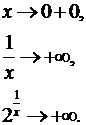
Следовательно, х = 0 — точка
разрыва второго рода (рис. 3).
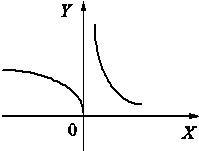
Рис. 3