Экстремумы функций многих переменных

Рассмотрим функцию n переменных .

Определение 12.13. Точка называется точкой локального максимума (минимума) функции, если найдется некоторая окрестность данной точки, для всех точек которой выполняется условие .

Определение 12.14. Точки локального максимума и минимума называются точками экстремума.

Теорема 12.6. (необходимое условие экстремума функции). Если точка является точкой локального экстремума функции, то в этой точке все частные производные равны нулю.

Доказательство. Пусть — точка экстремума функции. Для каждого рассмотрим функцию одной переменной.

.

Точка является точкой локального экстремума для функции , следовательно, в этой точке производная , тогда частная производная

.

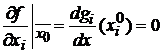Следовательно, в точке локального экстремума функции все частные производные равны нулю.

Определение 12.15. Точки, в которых частные производные равны нулю называются стационарными точками функции многих переменных.

Стационарные точки являются точками, "подозрительными" на экстремум.

Необходимое условие экстремума не является достаточным, т.е. не каждая стационарная точка является точкой экстремума.

Например, функция имеет частные производные

, .

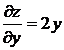В точке (0,0) частные производные функции равны нулю, однако в этой точке у функции нет экстремума. Данная точка является седловой точкой графика (рис. 12.6).

Определение 12.16. Матрица, составленная из значений частных производных второго порядка, вычисленных в некоторой точке называется матрицей Гессе

,

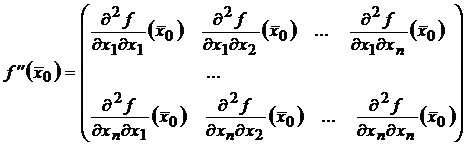или в сокращенном виде

.

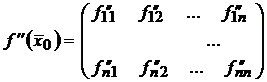Определение 12.17. Матрица Гессе называется положительно (отрицательно) определенной, если для любого вектора приращения справедливо соотношение .

Теорема 12.7. (критерий Сильвестра). Необходимым и достаточным условием положительной определенности матрицы Гессе является выполнение n условий:

,

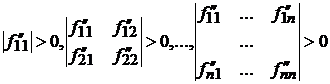т.е. необходимо и достаточно, чтобы все левые верхние миноры этой матрицы были положительны.

Необходимым и достаточным условием отрицательной определенности матрицы является выполнение следующих условий:

,

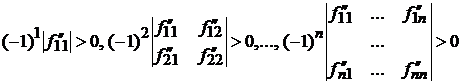т.е. необходимо и достаточно, чтобы левые верхние миноры нечетных порядков были отрицательны, а миноры четных порядков - положительны.

Теорема 12.8. (достаточное условие экстремума функции). Для того чтобы дважды непрерывно дифференцируемая функция имела в стационарной точке локальный минимум (максимум), необходимо и достаточно, чтобы матрица Гессе в этой точке была положительно (отрицательно) определена.

Пример 12.1. Исследовать на экстремум функцию двух переменных .

Решение. Найдем частные производные функции и приравняем их к нулю:

.

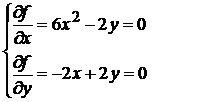Решив систему, получим две стационарные точки: и .

Составим матрицу Гессе для первой точки:

,

,

.

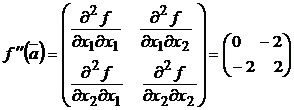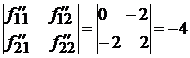Не выполнены условия положительной или отрицательной определенности, локального экстремума нет.

Составим матрицу Гессе для второй точки:

,

,

.

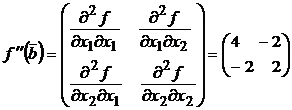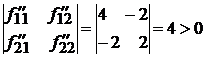Выполнено условие положительной определенности, в точке локальный минимум.