Частные производные высших порядков

Рассмотрим функцию двух переменных n=2, . Предположим, что функция имеет частные производные

, ,

которые являются функциями двух переменных. Их называют частными производными первого порядка. Предположим, что они дифференцируемы.

Определение 1. Частные производные от частных производных первого порядка называются частными производными второго порядка.

= , = .

= , = .

Две последние называют смешанными производными.

Если полученные функции являются дифференцируемыми, то частные производные от них называются частными производными третьего порядка. Например:

.

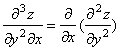Определение 2. Частной производной n-го порядка называется частная производная от частной производной (n-1)-го порядка. Частных производных n-го порядка от функции двух переменных 2ⁿ штук.

Частная производная порядка р функции имеет вид

, где .

Теорема. Если частные производные первого порядка некоторой функции непрерывно дифференцируемы, то результаты смешанного дифференцирования равны.

.

Пример. .

, ,

, , , ,

.