Производная
по направлению
Рассмотрим функцию двух переменных n=2; z=f(x, y).
Под направлением мы будем понимать любой вектор ![]() на плоскости.
на плоскости.

Определение 1. Направляющими
косинусами данного направления ![]() называются косинусы
углов, которые данное направление образуют с положительными направлениями осей
координат. Направляющие косинусы данного направления -
называются косинусы
углов, которые данное направление образуют с положительными направлениями осей
координат. Направляющие косинусы данного направления -![]() .
.
Направляющие косинусы любого
направления в любом пространстве обладают следующим свойством: сумма квадратов
направляющих косинусов равна единице.
![]() .
.
На плоскости имеем
![]() .
.
![]() .
.
Если рассмотреть вектор ![]() , координатами которого являются направляющие косинусы
данного направления, то этот вектор сонаправлен с вектором
, координатами которого являются направляющие косинусы
данного направления, то этот вектор сонаправлен с вектором ![]() и имеет единичную длину.
и имеет единичную длину.
Пусть даны точка ![]() и направление
и направление ![]() . Переместим точку М0 вдоль направления
. Переместим точку М0 вдоль направления ![]() на величину Dl в точку М1. Тогда функция и аргумент получат
соответствующие приращения.
на величину Dl в точку М1. Тогда функция и аргумент получат
соответствующие приращения.
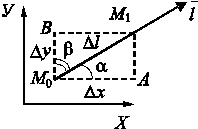
Функция получит приращение, которое называется приращением
функции в данном направлении: ![]() ,
,
Из
треугольника М0 М1 А: ![]() .
.
Из
треугольника М0
М1 В: ![]() .
.
![]() .
.
Определение 2. Предел
отношения приращения функции в данном направлении к приращению направления,
когда приращение направления стремится к нулю, называется производной функции в
данном направлении (если этот предел существует и конечен);
![]() .
.
Если направление ![]() совпадает с
направлением оси ОХ, то производная
по направлению совпадает с частной производной
по переменной х. Аналогично
производная по направлению оси ОУ совпадает с частной производной по
переменной у.
совпадает с
направлением оси ОХ, то производная
по направлению совпадает с частной производной
по переменной х. Аналогично
производная по направлению оси ОУ совпадает с частной производной по
переменной у.
Теорема. Производная по направлению
равна сумме попарных произведений частных производных в данной точке на
направляющие косинусы данного направления.
![]() .
.
Доказательство.
Приращение функции отличается от дифференциала на б.м. функции
более высокого порядка чем приращения аргументов.
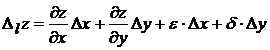 ,
,
где ![]() при
при ![]() соответственно.
Используя соотношения
соответственно.
Используя соотношения
![]() ,
, ![]() ,
,
получим:
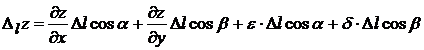 .
.
Разделим обе части на ![]()
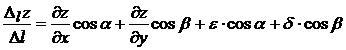
Перейдем в этом
равенстве к пределу при ![]() , при этом
, при этом ![]()
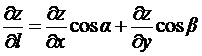 ,
,
что и требовалось
доказать. Доказательство для случая функции n
переменных ![]() и направления
и направления
![]() , заданного направляющими косинусами
, заданного направляющими косинусами ![]() проводится аналогично
проводится аналогично
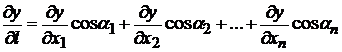 .
.
Пример. Найти производную функции ![]() в точке М(1, 2)
в направлении
в точке М(1, 2)
в направлении ![]() (4, -3).
(4, -3).
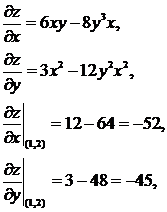
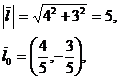
![]()
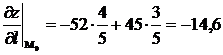 .
.