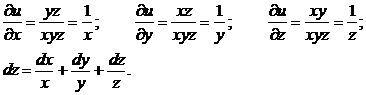Полный дифференциал

Определение. Полным дифференциалом функции многих переменных называется главная линейная относительно приращений аргументов часть малого полного приращения функции.

Рассмотрим функцию двух переменных n=2; z=f(x,y). Если приращение функции можно представить в виде

, (*)

где - бесконечно малые функции при , соответственно, то выражение называется полным дифференциалом функции двух переменных.

Теорема. Полный дифференциал равен сумме попарных произведений частных производных на дифференциалы соответствующих переменных.

.

Доказательство. В равенстве (*) положим . В левой части получим частное приращение функции по переменной x.

Разделим обе части на

Переходя к пределу в этом равенстве при , получим

.

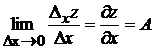Аналогично, полагая в равенстве (*) , имеем

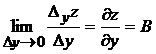
Подставляя выражения для А и В в (*) и учитывая, что получим

,

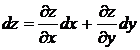что и требовалось доказать. Доказательство для случая функции n переменных проводится аналогично

.

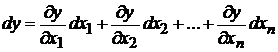Пример. .