Частные производные функции

многих переменных

Рассмотрим функцию двух переменных n=2; z=f(x,y).

Определение. Частной производной функции z=f(x,y) в точке (x₀, y₀)D(у) по соответствующей переменной называется предел отношения частного приращения функции по этой переменной к приращению этой переменной, когда приращение переменной стремится к нулю (если этот предел существует и конечен).

,

.

При введении частной производной по любой переменной остальные переменные были фиксированы. Данное определение совпадает с определением производной функции одной переменной. Следовательно, частную производную можно найти, зафиксировав все переменные, кроме одной, считая их постоянными. Производная находится как производная функции одной переменной, т.е. . Все правила и формулы, справедливые для производной функции одной переменной, остаются справедливыми и для частных производных.

Пример 1.

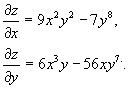
Пример 2.