Решение систем n линейных уравнений

с n неизвестными с помощью обратной матрицы

и по формулам Крамера

Пример 1. Решить систему уравнений с помощью обратной матрицы.

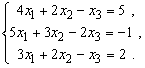
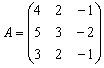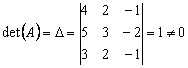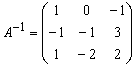Решение. Матрица невырожденная, так как , значит, существует обратная матрица. Вычислим обратную матрицу:. Тогда

,

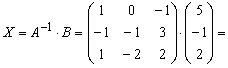
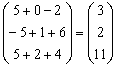т.е. .

Пример 2. Решить систему линейных уравнений по формулам Крамера:

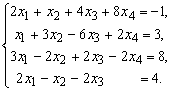
Составим и вычислим главный определитель системы:

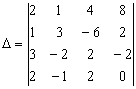
Создадим нули в четвертом столбце, для чего умножим на (–4) вторую строку и прибавим к первой, затем вторую строку прибавим к третьей, получим

и разложим полученный определитель по элементам четвертого столбца.

,

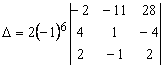вынесем из 1 и 3 столбцов 2, тогда

.

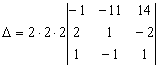Создадим нули в третьей строке, для чего первый столбец прибавим ко второму, а затем вычтем из третьего.

.

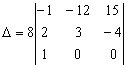Разложим определитель по элементам третьей строки:

.

Так как , то система имеет единственное определитель. Составим определитель , заменив в первый столбец столбцом свободных членов и вычислим его.

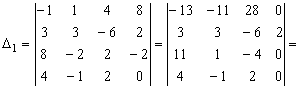
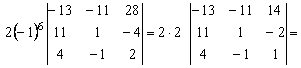
Находим определители .

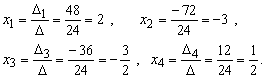
Ответ:

Пример 3. Решить матричное уравнение

.

Введем обозначения

, тогда уравнение примет вид

.

Найдем определитель матрицы А:

.

Матрица А невырожденная, поэтому для нее существует обратная матрица . Умножим матричное уравнение на матрицу слева: , . Матрица невырожденная. Найдем к ней обратную матрицу

.

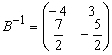Умножим матричное уравнение на справа, получим , , , т.е.

.
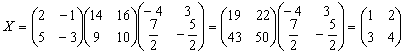