Системы линейных неоднородных уравнений

Определение. Система вида

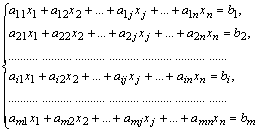
называется системой m линейных уравнений с n неизвестными.

В матричной форме система имеет вид

,

где

- матрица коэффициентов при переменных;

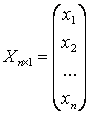
- матрица-столбец переменных;

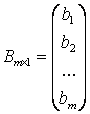
- матрица-столбец свободных членов.

Определение. Система называется однородной, если все свободные члены равны нулю, и неоднородной, если хотя бы один из свободных членов не равен нулю.

Определение. Решением неоднородной системы называется такая совокупность n чисел , при подстановке которых каждое уравнение системы обращается в верное равенство.

Определение. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.

Определение. Совместная система уравнений называется определенной, если она имеет одно решение, и неопределенной, если она имеет более одного решения.

Методы решения системы n линейных уравнений

с n переменными

Пусть дана неоднородная система n линейных уравнений с n неизвестными:

.

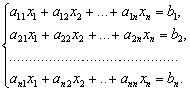а) Метод обратной матрицы.

Данную матрицу можно представить в матричном виде .

Допустим, что определитель матрицы, составленный из коэффициентов при переменных, не равен нулю, т.е. . Тогда матрица А имеет обратную матрицу . Умножив обе части равенства слева на , получим

, откуда или .

Таким образом, чтобы найти решение системы Х, надо найти обратную матрицу к матрице коэффициентов при неизвестных А и умножить ее справа на матрицу-столбец свободных членов В.

б) Формулы Крамера.

Теорема Крамера. Пусть ∆ - определитель матрицы системы А, а ∆_j - определитель матрицы, получаемой из матрицы А заменой j-го столбца столбцом свободных членов. Тогда если ∆ ≠ 0, то система имеет единственное решение, определяемое по формулам

,

где ∆ - главный определитель, ∆_j - вспомогательный определитель.

Следствия из теоремы:

1) если и хотя бы один из вспомогательных определителей не равен нулю, то система решений не имеет;

2) если и все , то система имеет бесконечно много решений.

Заметим, что решение систем n линейных уравнений с n неизвестными по формулам Крамера и методом обратной матрицы представляет в большей степени теоретический интерес, так как чаще приходится решать экономические задачи, содержащие системы m линейных уравнений с n неизвестными.

в) Метод Гаусса - метод последовательного исключения переменных.

Пусть дана неоднородная система m линейных уравнений с n неизвестными:

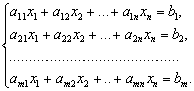
Метод последовательного исключения переменных состоит в приведении расширенной матрицы системы к ступенчатому виду путем последовательного исключения неизвестных с помощью элементарных преобразований.

Выпишем расширенную матрицу данной системы:

.

Определение. Расширенной матрицей называется матрица, составленная из матрицы коэффициентов при переменных А и дополненная матрицей-столбцом свободных членов В.

С помощью элементарных преобразований приведем полученную матрицу к ступенчатому виду:

.

Теорема Кронекера - Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы, т.е. .

Разрешимость системы линейных неоднородных уравнений относительно ранга матрицы этой системы представлена в виде схемы
(рис. 1).

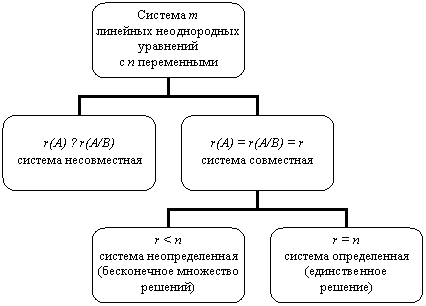
Рис. 1

Заметим, что при переменные называются основными (или базисными), если определитель матрицы из коэффициентов при них (базисный минор) отличен от нуля. Остальные n-r переменные называются свободными.

Определение. Выражение базисных переменных через свободные называется общим решением системы линейных уравнений.

Определение. Решение системы, полученное из общего при подстановке конкретных значений свободных переменных, называется частным решением системы линейных уравнений.

Определение. Частное решение системы линейных уравнений, полученное из общего при подстановке нулевых значений свободных переменных, называется базисным решением системы.

Определение. Базисное решение системы линейных уравнений, значения переменных которого неотрицательные, называется опорным решением системы.