Применение понятия

определенного интеграла в экономике

Производительность труда

Пусть описывает изменение производительности некоторого производства с течением времени.

Найти объем продукции Q, произведенной за промежуток времени .

Допустим, что производительность труда не изменяется с течением времени, тогда объем продукции ∆Q, произведенный за период времени , задается формулой . В общем случае справедливо приближенное равенство , где , которое становится более точным при уменьшении ∆t.

Разобьем отрезок на промежутки времени точками: . Для объема продукции ∆Q, произведенной за период времени , имеем , где , , . Тогда сумму приближенных равенств

,

каждое из которых становится более точным при

,

запишем в виде

.

Согласно определению определенного интеграла получим

. (1)

В последнем равенстве - производительность труда в момент t, а - объем выпускаемой продукции за промежуток времени .

Заметим, что в производственной функции Кобба - Дугласа затраты труда можно принять за линейную зависимость от времени и при этом считать затраты капитала неизменными. Тогда функция примет вид , а объем выпускаемой продукции за
Т лет составит:

. (2)

Пример 1. Найти объем продукции, произведенной за 4 года, если функция Кобба - Дугласа имеет вид .

Решение. По формуле

объем произведенной продукции

.

Используем метод интегрирования по частям.

Пусть ,. Тогда

, .

Следовательно:

.

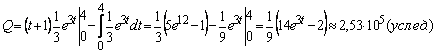Кривая обучения

Пусть - время, измеряемое в человеко-часах, необходимое для производства первых х ед. продукции.

Найти время, необходимое для производства единиц продукции с номерами от до n₂.

Рис. 1

Выражение приближенно равно значению времени, необходимого для производства -й единицы продукции. Как правило, используют функции вида , где , . График функции такого вида представлен на рис. 1 и называется кривой обучения.

Заметим, что функция - убывающая, так как время, необходимое для выполнения операции, убывает при возрастании числа повторов.

Время , необходимое для производства единиц продукции с номерами от до n₂, вычисляется по формуле

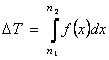. (3)

Пример 2. После сборки 100 часов оказалось, что в дальнейшем время убывает в соответствии с формулой Найти время, которое потребуется для сборки еще 20 часов (т.е. с номера 101 до номера 120).

Решение. В соответствии с формулой

можно записать изменения времени:

Средние значения

Пусть функция показывает изменение затрат времени t на изготовление изделия в зависимости от степени освоения производства, где х - порядковый номер изделия в партии.

Среднее время t_ср, затраченное на изготовление одного изделия в период от х₁ до х₂ изделий, вычисляется по теореме о среднем

,

т.е.

. (4)

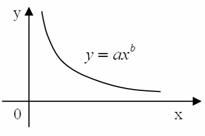
Заметим, что функция изменения затрат времени на изготовление изделий часто имеет вид , где а - затраты времени на первое изделие, b - показатель производственного процесса.

Пример 3. Найти среднее время, затраченное на освоение одного изделия в период освоения от х₁ = 100 до х₂ = 121 изделий, полагая в формуле

а = 600 (мин), b=0,5.

Решение. Используя формулу

,

получим

.

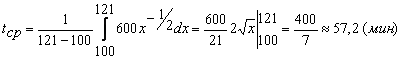Дисконтирование

Определение. Дисконтированием называется процесс вычисления начальной суммы S по ее конечной величине S_t, полученной через t лет при годовой процентной ставке р.

При непрерывном начислении процента конечная сумма вычисляется по формуле , где .

Пусть сумма - функция от времени, тогда дисконтированная сумма к моменту времени t составит , откуда .

Чтобы вычислить величину S, разделим отрезок времени t на n равных отрезков времени ∆t. В малом отрезке времени ∆t доход можно считать неизменным и, следовательно, равным . При непрерывном начислении процентов дисконтированный доход составит .

В отрезке времени дисконтированный доход составит

.

Полная дисконтированная сумма за период времени t вычисляется по формуле

. (5)

Пример 4. Определить дисконтированный доход за три года при процентной ставке 8%, если первоначальные (базовые) капиталовложения составили 10 млн. руб. и намечается ежегодно увеличивать капиталовложения на 1 млн. руб.

Решение. Очевидно, что капиталовложения задаются функцией . Тогда по формуле

дисконтированная сумма капиталовложений

.

Интегрируя, получим (млрд. руб.). Это означает, что для получения одинаковой наращенной суммы через три года ежегодные капиталовложения от 10 до 13 млн. руб. равносильны одновременным первоначальным вложениям 30,5 млн. руб. при той же, но начисляемой непрерывно процентной ставке.

Капитал (основные фонды) и чистые инвестиции

Пусть К(t) - функция капитала, зависящая от времени, а I(t) - чистые инвестиции, т.е. общее увеличение капитала с вычетом средств, идущих на возмещение выходящих из строя основных фондов (капитала). Иначе, за единицу времени капитал увеличивается на величину чистых инвестиций. Тогда

- производная от капитала по времени t.

Чтобы найти приращение капитала за период времени от t₁ до t₂, т.е. величину , воспользуемся формулой, связывающей первообразную К(t) с определенным интегралом:

. (6)

Неравномерное распределение дохода

Пусть функция характеризует неравномерность распределения доходов среди населения, где у – доля совокупного дохода, получаемая частью х наиболее низкооплачиваемого населения.

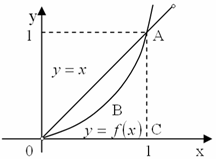
Рис. 2

График рассматриваемой функции называется кривой Лоренца (рис. 2.3), где , , . Исследуя кривую Лоренца, отражающую зависимость процента доходов от процента имеющего их населения, можно оценить степень неравенства в распределении доходов населения.

Заметим, что при равномерном (идеальном) распределении доходов кривая Лоренца представляет собой прямую - биссектрису ОА.

Определение. Отклонение реального распределения доходов от идеального, выражающееся отношением площади между прямой и кривой Лоренца к площади, ограниченной прямыми , и осью Ох, называется коэффициентом неравномерности распределения доходов (коэффициентом Джини).

Очевидно, что неравномерность распределения доходов тем больше, чем больше площадь фигуры ОАВ (рис. 2).

Пример 5. Распределение доходов в одной из стран описывается уравнением

, где .

Определить коэффициент Джини k.

Решение. Согласно формуле

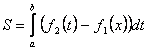
получим площадь фигуры ОАВ (рис. 2.3):

Площадь треугольника ОАС:

.

Тогда

.

Потребительский излишек (CS)

Определение. Потребительский излишек (добавочная выгода потребителя) - превышение общей стоимости, которую потребитель готов уплатить за все единицы товара, над его реальными расходами на их приобретение.

Рис. 3	Пусть Р0 - равновесная цена, Q0 - количество товара, реализуемого по этой цене, тогда - реальные затраты на товар в условиях рынка. Определение. Точка равновесия - это точка пересечения кривых спроса и предложения, а соответствующая ей цена - равновесная цена.
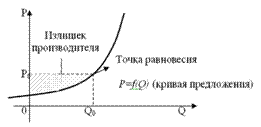
Рис. 4	Заметим, что в точке равновесия весь произведенный товар находит своего покупателя и все желающие могут купить данный товар (рис. 3). Согласно кривой спроса (рис. 4), потребитель может оплатить товар по различным ценам, так как товар

в количестве Q₀ не сразу весь попадает на рынок, а выбрасывается небольшими партиями, равными ∆Q. Задача продавца - поддержать цену на товар выше равновесной.

Очевидно, что общие затраты потребителей на все количество товара Q₀ будут составлять

.

При ∆Q→0 суммарные затраты потребителей будут равны площади криволинейной трапеции между точками 0 и Q₀:

.

Согласно определению, излишек потребителя - это разность между предполагаемыми и реальными затратами потребителей в условиях рынка, т.е. . (7)

Заметим, что экономистов больше интересует величина изменения излишков потребителя в результате проведения мероприятий государственной политики (установление налогов, введение субсидий и т.д.), оказывающих влияние на равновесие рынка. Результат подобных изменений добавочной выгоды потребителя вычисляется по следующей формуле:

. (8)

Пример 6. Кривая спроса задана уравнением

, а равновесное количество товара Q₀=2. Найти излишек потребителя.

Решение. Найдем равновесную цену при Q₀=2:

.

Зная формулу для добавочной выгоды потребителя

,

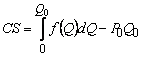получим

(ед.).

Излишек производителя (РS)

Определение. Излишек производителя (добавочная выгода производителя) - разность между той денежной суммой, за которую он был готов продать товар, и реальными доходами за реализованный товар.

Рис. 5

Пусть Р0 - равновесная цена, Q0 - количество товара, реализуемого по этой цене, тогда - доход за весь товар Q0, реализованный по цене Р0. Согласно кривой предложения (рис. 5), товар в количестве, меньшем Q0, производитель реализует по цене ниже Р0.

Рис. 2.4.

Очевидно, что область, представляющая добавочную выгоду производителя, вычисляется по формуле

. (9)

Пример 7. Определить добавочную выгоду производителя, если кривая предложения имеет вид , а точка равновесия достигается при .

Решение. Найдем равновесную цену при Q₀=4:

.

Зная формулу для добавочной выгоды производителя

,

получим

Пример 8. Известны законы спроса и предложения:

Найти выигрыш потребителей и выигрыш поставщиков, если было установлено рыночное равновесие.

Решение. Найдем точку рыночного равновесия из равенства p=s:

,

или , откуда

.

При х₀=9 равновесная цена составит , тогда доход на весь товар .

Зная формулу выгоды потребителя

и формулу выгоды производителя

,

получим

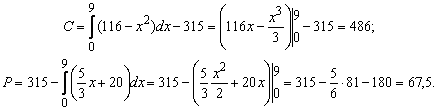
Пример 9. Скорости изменения издержек и дохода во времени имеют следующий вид: Найти максимальное значение прибыли, которое можно получить от этого производства.

Решение. Найдем скорость изменения прибыли из выражения

.

Максимальное значение прибыли достигается в точке максимума.

Приравняем производную прибыли к нулю, т.е. или , откуда .

Согласно второму достаточному условию экстремума, (), - точка максимума. Максимальное значение прибыли, которое можно получить от производства при t=5: