Непосредственное интегрирование
Вычисление
неопределенных интегралов с помощью таблицы интегралов и их основных свойств
называется непосредственным интегрированием.
Пример
1. Найдем интеграл
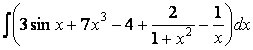 .
.
Применив второе
и пятое свойства неопределенного интеграла, получим
![]()
![]() . (*)
. (*)
Далее,
используя формулы II, Ш, IV, VIII таблицы и третье свойство интегралов, находим каждый из слагаемых
интегралов отдельно:
![]() =
=![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
Подставим эти
результаты в (*) и, обозначив сумму всех постоянных (ЗС1+7С2+4С3+2С4+С5) буквой С,
получим окончательно:
![]()
![]()
Проверим
результат дифференцированием. Найдем производную
полученного выражения:
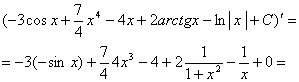
![]()
Мы получили
подынтегральную функцию, это доказывает, что интегрирование выполнено верно.
Пример 2. Найдем
![]() .
.
В таблице интегралов приведено следствие IIIа из формулы III:
![]()
Чтобы
воспользоваться этим следствием, найдем дифференциал
функции, стоящей в показателе степени:

Для создания этого дифференциала достаточно домножить знаменатель
дроби под интегралом на число 2 (очевидно, чтобы дробь не изменилась,
необходимо при этом умножить на 2 и числитель). После вынесения постоянного
множителя за знак интеграла он становится готовым для применения табличной
формулы IIIа:
![]() .
.
Проверка:
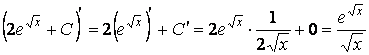 ,
,
следовательно,
интегрирование выполнено правильно.
Пример 3. Найдем
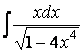 .
.
Так как из
выражения, стоящего в числителе, можно сконструировать дифференциал
квадратичной функции, то следует выделить в знаменателе такую функцию:
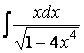
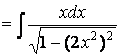 .
.
Для создания ее
дифференциала ![]() достаточно умножить числитель на 4 (знаменатель при этом также
умножим на 4 и вынесем этот множитель знаменателя за интеграл). В
результате мы получим возможность использовать табличную формулу X:
достаточно умножить числитель на 4 (знаменатель при этом также
умножим на 4 и вынесем этот множитель знаменателя за интеграл). В
результате мы получим возможность использовать табличную формулу X:
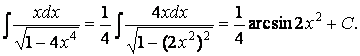
Проверка:
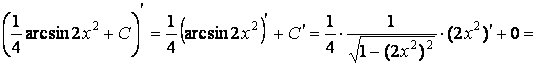
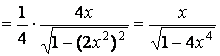 ,
,
т.е. интегрирование выполнено верно.
Пример 4. Найдем
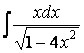 .
.
Заметим, что теперь квадратичная функция,
дифференциал которой ![]() можно создать в
числителе, является подкоренным выражением. Поэтому разумно будет записать
подынтегральную функцию как степенную, чтобы воспользоваться формулой I таблицы интегралов:
можно создать в
числителе, является подкоренным выражением. Поэтому разумно будет записать
подынтегральную функцию как степенную, чтобы воспользоваться формулой I таблицы интегралов: 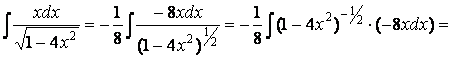

Проверка:

Вывод: интеграл
найден правильно.
Пример5. Найдем
![]()
Обратим
внимание на то, что подынтегральное выражение содержит
функцию ![]() ; и ее
дифференциал
; и ее
дифференциал ![]() . Но дробь
. Но дробь ![]() является также и
дифференциалом всего подкоренного выражения (с точностью до знака):
является также и
дифференциалом всего подкоренного выражения (с точностью до знака): ![]()
Поэтому разумно
представить дробь в виде степени:
![]()
Тогда после домножения числителя и знаменателя на (-1) мы получим
степенной интеграл (табличная формула I): 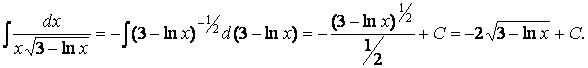
Дифференцированием
результата убеждаемся, что интегрирование выполнено верно.
Пример 6. Найдем
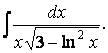
Легко
убедиться, что в этом интеграле из выражения
![]() дифференциал
подкоренной функции не удастся получить с помощью числовых коэффициентов.
Действительно,
дифференциал
подкоренной функции не удастся получить с помощью числовых коэффициентов.
Действительно,
![]() ,
,
где k —константа. Зато, по опыту примера 3, можно
сконструировать интеграл, совпадающий по виду с формулой X из таблицы интегралов:
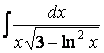
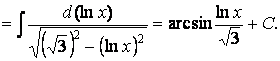
Пример
7. Найдем
![]()
![]()
Обратим внимание
на то, что в числителе легко создается дифференциал кубической функции d(x3) = 3x2dx. После чего мы получаем возможность использовать табличную формулу VI:
![]()
![]()
Пример 8. Найдем
![]()
Известно, что
производной функции arcsin x
является дробь
![]()
тогда
![]() .
.
Это приводит
нас к выводу, что искомый интеграл имеет вид степенного интеграла: ![]() , в котором и = arcsin x, a значит,
, в котором и = arcsin x, a значит,
![]()
Пример
9. Для
нахождения
![]()
воспользуемся
той же табличной формулой I и тем, что
![]() .
.
Получим
![]()
Пример
10. Найдем
![]()
Поскольку выражение ![]() является дифференциалом функции
является дифференциалом функции ![]() , то, используя формулу I таблицы интегралов, получаем
, то, используя формулу I таблицы интегралов, получаем ![]()
![]()
Пример
11. Для нахождения
интеграла
![]()
воспользуемся
последовательно: тригонометрической формулой
![]() ,
,
тем фактом, что
![]()
и формулой II таблицы интегралов:
![]()
Пример 12. Найдем
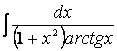 .
.
Так как
выражение
![]()
является
дифференциалом функции ![]() , то, используя ту
же формулу II, получаем
, то, используя ту
же формулу II, получаем
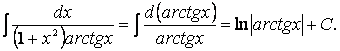
Пример
13. Найдем интеграл
![]() .
.
Заметим, что степень
переменной в числителе на единицу меньше, чем в знаменателе. Это позволяет в
числителе создать дифференциал знаменателя. Найдем
![]() .
.
После вынесения
постоянного множителя за знак интеграла домножим числитель и знаменатель подынтегральной
дроби на (-7), получим:
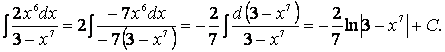
(Здесь
использовалась та же формула II из таблицы
интегралов).
Пример 14. Найдем интеграл
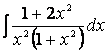 .
.
Представим
числитель в ином виде: 1 + 2х2
= (1 + х2) + х2 и
выполним почленное деление, после чего используем пятое свойство интегралов и
формулы I и VIII таблицы:

![]()
Пример 15. Найдем
![]() .
.
Вынесем
постоянный множитель за знак интеграла, вычтем и прибавим в числителе 5, затем
выполним почленное деление числителя на знаменатель и воспользуемся пятым
свойством интеграла:
![]()
Для вычисления первого интеграла используем третье свойство интегралов,
а второй интеграл представим в виде, удобном для применения формулы IX: 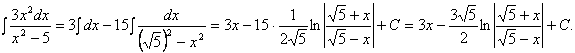
Пример 16. Найдем
![]() .
.
Отметим, что
показатель степени переменной в числителе на единицу меньше, чем в знаменателе
(что характерно для производной), а значит, в числителе можно сконструировать
дифференциал знаменателя. Найдем дифференциал выражения, стоящего в
знаменателе:
d(x2 - 5)=(х2 -5)'dx=2xdx.
Для получения в числителе дифференциала знаменателя не хватает
постоянного множителя 2. Умножим и разделим подынтегральную функцию на 2 и
вынесем постоянный множитель -
за знак
интеграла
![]()
Здесь мы использовали II табличный интеграл.
Рассмотрим
подобную же ситуацию в следующем примере.
Пример
17. Найдем
![]() .
.
Вычислим
дифференциал знаменателя:
![]() .
.
Создадим его в
числителе с помощью четвертого свойства интегралов:
![]() =
=
=![]()
Более сложная
подобная ситуация будет рассмотрена в примере 19.
Пример 18, Найдем
![]() .
.
Выделим в знаменателе полный квадрат:
![]()
Получим
![]() .
.
После выделения полного квадрата в знаменателе мы получили интеграл, близкий по виду к формулам VIII и IX таблицы интегралов, но в знаменателе формулы VIII слагаемые полные квадраты имеют одинаковые знаки, а в знаменателе нашего интеграла знаки слагаемых различны, хотя и не совпадают со знаками девятой формулы. Добиться полного совпадения знаков слагаемых в знаменателе со знаками в формуле IX удается вынесением коэффициента (-1) за интеграл. Итак, чтобы применить формулу IX таблицы интегралов, проведем следующие мероприятия:
1) вынесем (-1) за скобки в знаменателе и затем за интеграл;
2) найдем
дифференциал выражения
![]()
![]() ;
;
3) создадим в числителе найденный дифференциал;
4) представим
число 2 в виде, удобном для применения формулы IX таблицы: ![]()
Тогда
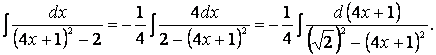
Используя
IX формулу
таблицы интегралов, получим
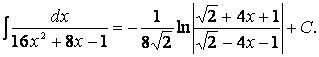
Пример 19. Найдем
![]() .
.
Используя опыт, приобретенный при отыскании интегралов в предыдущих
двух примерах, и полученные в них результаты, будем иметь ![]()
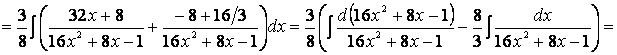
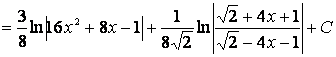 .
.
Обобщим некоторый опыт, полученный в результате решения примеров 17,18,19.
Итак, если мы
имеем интеграл вида
![]()
(пример 18), то, выделив полный квадрат в знаменателе, можно прийти к одной из табличных формул VIII или IX.
Интеграл же
вида
![]()
(пример 19) после создания в числителе производной знаменателя
распадается на два интеграла: первый – вида
![]()
(пример 17), берущийся по формуле П, и
второй —вида
![]()
(пример 18), берущийся по одной из формул VIII или IX.
Пример 20. Найдем
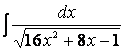 .
.
Интеграл вида
![]()
можно свести к
виду табличных формул X или XI, выделив в подкоренном выражении полный
квадрат. В нашем случае
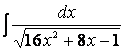 =
=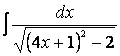 .
.
Подкоренное выражение
имеет вид выражения
![]() , где
, где ![]() .
.
Для применения
формулы
XI в числителе должен стоять дифференциал
![]() ;
;
поэтому следует
создать его, домножив числитель и знаменатель дроби на число 4:
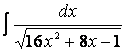
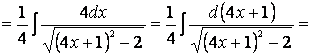
![]()
Пример 21. Найдем теперь
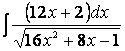 .
.
Используя опыт предыдущих примеров, создадим в числителе дифференциал знаменателя и разобьем интеграл на два, вынеся ненужные числовые коэффициенты за интегралы:
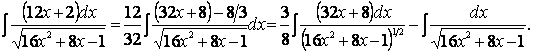
Первый интеграл
перепишем в виде степенного (т.е. в виде ![]() ), a второй был уже
взят нами в предыдущем примере, поэтому
), a второй был уже
взят нами в предыдущем примере, поэтому
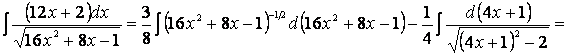
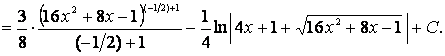
Пример 22. Найдем
![]() .
.
Так как sin x
является производной выражения (-соs x), то, отделив под интегралом одну степень
sin x , легко можно создать дифференциал функции cos x:
![]()
![]()
Теперь
выразим sin2 x через
cos x и
внесем знак минус в скобки:
![]()
![]()
Используя первое и пятое свойства интегралов, а также табличную формулу I, получаем:
![]()
![]()
Аналогично поступают всегда при вычислении интегралов вида
![]() ,
,
если один из показателей степени
положительное нечетное число, а
второй—произвольное действительное число (пример 23).
Пример
23. Найдем
![]() .
.
Используя опыт предыдущего примера и тождество
cos4x = (cos2 x)2 = (l — sin2x)2 = 1— 2sin2 x + sin4 x,
получим
![]()
Выполнив
почленное деление слагаемых числителя на знаменатель, будем иметь
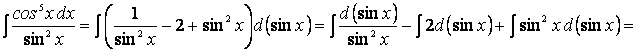
![]()
![]()
При
интегрировании четных степеней тригонометрических функций сначала следует по
возможности понизить степень, используя известные формулы:
2sin2 φ = l—cos2
φ, 2cos2 φ
= l + cos2φ
и 2 sinφ cosφ= sin2φ.
Пример
24. Найдем
![]() .
.
Преобразуем
подынтегральную функцию:
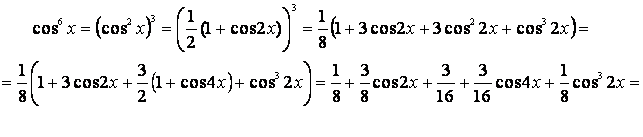
![]()
Подставив
полученную сумму под интеграл, получим
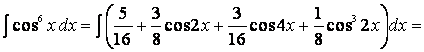
![]()
![]()
![]()
![]()
![]()