Задачи с ограничениями-неравенствами.
Условия Куна-Таккера
Задачи математического программирования, в которых ограничения могут быть заданы с помощью уравнений и неравенств, принято называть задачами нелинейного программирования. Эти задачи будем рассматривать в виде
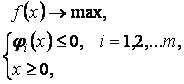 (1)
(1)
где ![]() - дважды непрерывно
дифференцируемые функции векторного аргумента
- дважды непрерывно
дифференцируемые функции векторного аргумента ![]() .
.
Заметим,
что представление задач нелинейного программирования в виде (1) не умаляет
общности дальнейших рассуждений. Действительно, максимизация ![]() тождественна
минимизации
тождественна
минимизации ![]() . Знак неравенства
. Знак неравенства ![]() также совершенно
условен, поскольку умножением обеих частей неравенства на
также совершенно
условен, поскольку умножением обеих частей неравенства на ![]() его можно развернуть в
противоположную сторону. Если случится ограничение-уравнение, то его можно
записать в виде двух неравенств, поскольку
его можно развернуть в
противоположную сторону. Если случится ограничение-уравнение, то его можно
записать в виде двух неравенств, поскольку
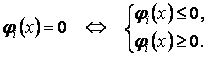
Если какая-либо
переменная ![]() является свободной, то
ее можно записать как разность двух неотрицательных переменных:
является свободной, то
ее можно записать как разность двух неотрицательных переменных: ![]() , где
, где ![]() . Если на нее наложено одностороннее нижнее ограничение, т.е.
. Если на нее наложено одностороннее нижнее ограничение, т.е.
![]() , то можно ввести переменную
, то можно ввести переменную ![]() и сделать замену по
формуле
и сделать замену по
формуле ![]() . Если же
. Если же ![]() , то
, то ![]() .
.
Задачи с неотрицательными
переменными. Для начала рассмотрим задачу нелинейного программирования,
в которой ограничения сводятся лишь к требованию неотрицательности переменных:
![]() (2)
(2)
Теорема 1. Если ![]() - решение задачи (2),
то для всех
- решение задачи (2),
то для всех ![]()
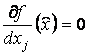 , если
, если ![]() , (3)
, (3)
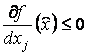 , если
, если ![]() . (4)
. (4)
Доказательство.
Поскольку ![]() - решение задачи, то
непременно является точкой локального максимума. Значит, для любого
- решение задачи, то
непременно является точкой локального максимума. Значит, для любого ![]() выполняется неравенство
выполняется неравенство
![]() . Если
. Если ![]() , значит принадлежит допустимой области вместе с некоторой
своей
, значит принадлежит допустимой области вместе с некоторой
своей ![]() -окрестностью. В этом случае, как было доказано выше,
-окрестностью. В этом случае, как было доказано выше, ![]() . Допустим, теперь, что какая-то переменная принимает
граничное значение
. Допустим, теперь, что какая-то переменная принимает
граничное значение ![]() . Для нее возможно только неотрицательное приращение
. Для нее возможно только неотрицательное приращение ![]() . Но чтобы это приращение не приводило к нарушению
соотношения
. Но чтобы это приращение не приводило к нарушению
соотношения![]() необходимо, чтобы производная по этой переменной была неположительна.
необходимо, чтобы производная по этой переменной была неположительна.
Теорема
доказана.
Нетрудно
видеть, что условия (3) и (4) можно записать в следующей форме:
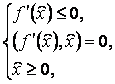 (5)
(5)
где 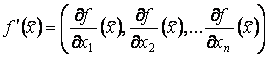 .
.
Замечание 1. Условия (5)
дают признак максимума. В случае минимума, необходимо, чтобы выполнялось
условие ![]() .
.
Достаточность
проверяется так же, как в задачах безусловной оптимизации, т.е. по критерию Сильвестра. Но учитывать при этом
следует лишь те переменные, производные которых в исследуемой точке равны нулю.
Пример 1. Покажем, что ![]() - решение задачи
- решение задачи
![]() .
.
Во-первых,
как видим, ![]() . Во-вторых, градиент
также неотрицателен:
. Во-вторых, градиент
также неотрицателен:
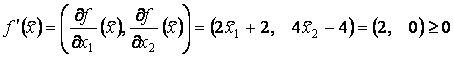 .
.
Более
того, ![]() . Следовательно, все необходимые условия минимума
выполняются. Проверим выполнение достаточных условий. Поскольку
. Следовательно, все необходимые условия минимума
выполняются. Проверим выполнение достаточных условий. Поскольку ![]() , вычислим для нее вторую производную, убедимся, что она
положительна.
, вычислим для нее вторую производную, убедимся, что она
положительна.
 .
.
Условия Куна-Таккера. Вернемся
к задаче (1) и рассмотрим ее, используя результаты, полученные для задачи (2).
Теорема 2. Если ![]() есть решение задачи (1),
то найдутся множители
есть решение задачи (1),
то найдутся множители ![]() , такие что для
, такие что для ![]()
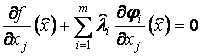 , если
, если ![]() , (6)
, (6)
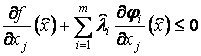 , если
, если ![]() , (7)
, (7)
и для ![]()
![]() , если
, если ![]() , (8)
, (8)
![]() , если
, если ![]() . (9)
. (9)
Доказательство.
Преобразуем ограничения-неравенства в уравнения. Для этого введем в задачу
дополнительные неотрицательные переменные ![]() . Очевидно, для всех
. Очевидно, для всех ![]()
![]()
![]()
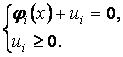
Далее,
используя функцию Лагранжа, сводим задачу (1)
к виду (2):
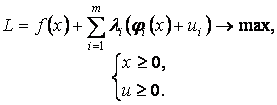
Записывая
для этой задачи условия (5) с учетом того, что ![]() , получаем так называемые
условия Куна-Таккера:
, получаем так называемые
условия Куна-Таккера:
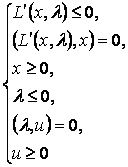
![]()
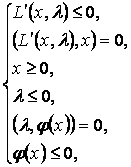 (10)
(10)
где
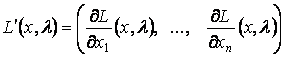 ,
,
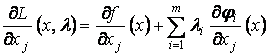 .
.
Нетрудно видеть, что (10) есть не что иное, как компактная форма записи условий (6) - (9).
Теорема
доказана.
Пример 2. Рассмотрим задачу
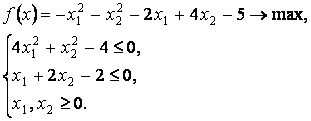
Исследуем
целевую функцию, вычислив для нее градиент и матрицу
Гессе.
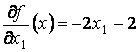 ;
; 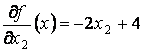 ;
;
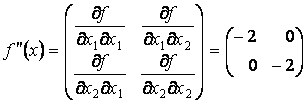 .
.
Как
видим, матрица Гессе отрицательно определена при любом ![]() , значит, целевая функция выпукла вверх. Аналогично можно
показать выпуклость допустимого множества. Таким образом, задача в целом
выпукла и, следовательно, имеет единственное решение в точке, удовлетворяющей
условиям Куна-Таккера.
, значит, целевая функция выпукла вверх. Аналогично можно
показать выпуклость допустимого множества. Таким образом, задача в целом
выпукла и, следовательно, имеет единственное решение в точке, удовлетворяющей
условиям Куна-Таккера.
Функция
Лагранжа:
![]() .
.
Условия
Куна-Таккера:
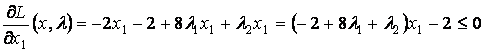 ,
,
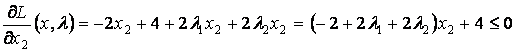 ,
,
![]() =
=![]() +
+![]() ,
,
![]()
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() .
.
Эти
условия годятся лишь для того, чтобы проверить экстремальность предлагаемых
точек, но не для того, чтобы построить алгоритм их поиска. Поэтому для примера
рассмотрим две точки: ![]() и
и ![]() . Подстановкой можно убедиться, что обе они удовлетворяют системе
ограничений. Одна из них является решением задачи. Определим, какая именно.
. Подстановкой можно убедиться, что обе они удовлетворяют системе
ограничений. Одна из них является решением задачи. Определим, какая именно.
1)
Рассмотрим точку ![]() . Поскольку
. Поскольку ![]() , необходимо, чтобы выполнялось условие
, необходимо, чтобы выполнялось условие ![]() . Воспользуемся этим, чтобы найти
. Воспользуемся этим, чтобы найти ![]() .
.
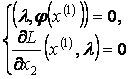
![]()
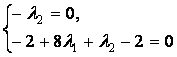
![]()
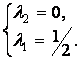
Условие
![]() не выполняется.
Следовательно,
не выполняется.
Следовательно, ![]() не является решением.
не является решением.
2)
Рассмотрим точку ![]() . Поскольку
. Поскольку ![]() , необходимо, чтобы выполнялось условие
, необходимо, чтобы выполнялось условие ![]() . Находим
. Находим ![]() :
:
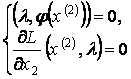
![]()
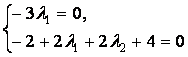
![]()
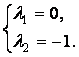
Как
видим, ![]() . Все условия Куна-Таккера выполняются, следовательно,
. Все условия Куна-Таккера выполняются, следовательно, ![]() - решение задачи.
- решение задачи.