Экстремумы ФНП

Введем понятия максимума и минимума для функции двух переменных .

При этом под окрестностью точки будем понимать любой круг с центром в точке .

Определение. Говорят, что непрерывная функция в точке имеет максимум (минимум), если в некоторой проколотой окрестности точки выполняется неравенство (), т.е. значение является наибольшим (наименьшим) в этой окрестности.

Необходимое условие существования экстремума аналогично необходимому условию экстремума функции одной переменной.

Если в точке функция имеет экстремум (максимум или минимум) и существуют частные производные и , то обе они равны нулю.

Это условие не является достаточным. Так, функция в точке имеет обе частные производные, равные нулю: , , но экстремума в этой точке она не имеет, так как на линии при , а на линии при .

С другой стороны, функция двух переменных (по аналогии с функцией одной переменной) может иметь экстремум и в точках, в которых обе частные производные не существуют.

Так функция в точке не имеет частных производных по и по , так как , , а функция не имеет производной в точке .

Но в точке рассматриваемая функция имеет очевидный минимум. Ее значения в любой проколотой окрестности точки удовлетворяют неравенству .

Для формулировки достаточного условия существования экстремума функции двух переменных введем понятие частных производных второго порядка.

Определение. Частная производная от частной производной функции любого числа переменных называется ее частной производной второго порядка.

Для функции двух переменных можно сконструировать такие частные производные второго порядка

, , , .

Например, для функции

, ,

, , , .

Заметим, что частные производные и , отличающиеся друг от друга только порядком дифференцирования, оказались равными. И это не случайно, так как для таких производных справедливо утверждение об их равенстве в любой точке, в которой они непрерывны.

Следующая теорема дает достаточное условие существования экстремума функции двух переменных.

Теорема. Пусть в точке обе частные производные первого порядка и равны нулю; числа , , есть значения в точке производных второго порядка , , ; число .

Тогда, если:

1) , то в точке функция имеет экстремум, причем максимум, если , и минимум, если ;

2) , в точке функция не имеет экстремума;

3) , то вопрос остается открытым (экстремум в точке может быть, а может его и не быть).

Пример. Исследуйте на экстремум функцию .

Решение.

Из системы уравнений 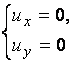найдем точки, в которых функция может иметь экстремум (критические точки):

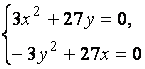
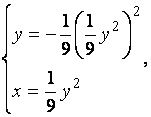
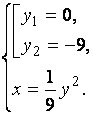
Получили две критические точки , .

В точке , , ,

.

Значит, в точке функция не имеет экстремума.

В точке ,, ,

.

Следовательно, в точке функция имеет экстремум, причем минимум, так как .

Вычислим значение функции в точке :

.

Итак, данная функция имеет единственный экстремум - минимум в точке , равный .