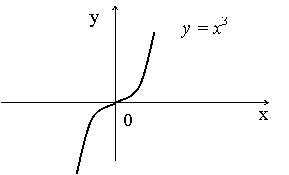Отыскание экстремумов функций
Определение. Говорят,
что функция ![]() , непрерывная в некотором промежутке
, непрерывная в некотором промежутке ![]() , имеет в точке
, имеет в точке ![]() максимум (минимум),
если существует проколотая окрестность точки
максимум (минимум),
если существует проколотая окрестность точки ![]() , в которой выполняется неравенство
, в которой выполняется неравенство ![]()
![]() .
.
Значения
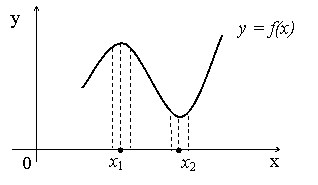
функции в точке максимума (минимума) функции называются, соответственно, максимумом и минимумом функции. Максимумы и минимумы объединяют общим названием экстремумов функции. На рисунке функция ![]() имеет максимум в точке
имеет максимум в точке
![]() и минимум в точке
и минимум в точке ![]() :
:
|
|
|
Экстремум функции часто называют локальным экстремумом, имея в виду, что
он характеризует поведение функции лишь в достаточно малой окрестности точки ![]() .
.
Функция может иметь несколько экстремумов в одном
промежутке, в отличие от так называемых глобального
максимума и глобального минимума,
т.е. наибольшего и наименьшего значений функции на всем промежутке.
Необходимое
условие существования экстремума выявляется следующим рассуждением: если дифференцируемая функция в точке ![]() имеет экстремум, то в
некоторой окрестности точки
имеет экстремум, то в
некоторой окрестности точки ![]() она удовлетворяет
условиям теоремы Ферма и, следовательно, в этой точке производная равна нулю,
т.е.
она удовлетворяет
условиям теоремы Ферма и, следовательно, в этой точке производная равна нулю,
т.е. ![]() .
.
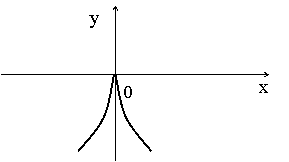
Заметим,
что функция может иметь экстремумы и в точках, в которых она не дифференцируема.
Например, функция ![]() имеет минимум в точке
имеет минимум в точке ![]() , но не дифференцируема в этой точке.
, но не дифференцируема в этой точке.
|
|
А функция |
Теперь
необходимое условие существования экстремума будет выглядеть так: если функция имеет экстремум в точке ![]() , то в этой точке ее производная равняется нулю или не
существует.
, то в этой точке ее производная равняется нулю или не
существует.
Точки, принадлежащие области определения, в которых выполняется
необходимое условие существования экстремума, принято называть критическими точками функции.
Однако необходимое условие существования экстремума не является
достаточным.
|
|
Например, для функции |
Поэтому
нужны достаточные условия существования экстремума.
Первое достаточное условие существования
экстремума дается следующей теоремой.
Пусть функция ![]() дифференцируема, по
крайней мере, в проколотой окрестности критической точки
дифференцируема, по
крайней мере, в проколотой окрестности критической точки ![]() и ее производная
сохраняет знак в каждой из полуокрестностей. Тогда: 1) если при переходе через
точку
и ее производная
сохраняет знак в каждой из полуокрестностей. Тогда: 1) если при переходе через
точку ![]() производная меняет
знак с плюса на минус, то
производная меняет
знак с плюса на минус, то ![]() - точка максимума; 2) если при переходе через точку
- точка максимума; 2) если при переходе через точку ![]() производная меняет
знак с минуса на плюс, то
производная меняет
знак с минуса на плюс, то ![]() - точка минимума; 3) если при переходе через точку
- точка минимума; 3) если при переходе через точку ![]() производная не меняет знака,
то в точке
производная не меняет знака,
то в точке ![]() нет экстремума.
нет экстремума.
Утверждение становится понятным, если учесть достаточное условие монотонности
функции. Так, например, в случае 1) функция возрастает в левой полуокрестности
и ее значения меньше ![]() и убывает в правой и ее значения здесь также меньше
и убывает в правой и ее значения здесь также меньше ![]() , т.е.
, т.е. ![]() - максимум
функции. Аналогичная ситуация в случае 2). Если же имеет место случай 3), то
функция либо возрастает, либо убывает во всей окрестности точки
- максимум
функции. Аналогичная ситуация в случае 2). Если же имеет место случай 3), то
функция либо возрастает, либо убывает во всей окрестности точки ![]() и
и ![]() не является точкой
экстремума.
не является точкой
экстремума.
На основании первого достаточного условия
экстремума можно составить план исследования функции на экстремум:
1. Найти
область определения функции ![]() , если она не указана.
, если она не указана.
2. Найти производную ![]() .
.
3. Найти критические точки
функции.
4. Выяснить знак производной
слева и справа от каждой критической точки и сделать вывод о наличии (или
отсутствии) экстремумов функции.
5. Вычислить экстремальные
значения.
Заметим, что практически удобно соединять
исследование функции на монотонность с исследованием ее на экстремум. При этом
результаты вычислений можно оформить в виде таблицы.
Пример 1. Исследуйте на экстремум и монотонность функцию
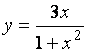 .
.
Решение.
1. Функция определена в
интервале ![]() .
.
2. 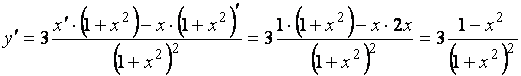 .
.
3. ![]() существует в
существует в ![]() и обращается в нуль в
точках
и обращается в нуль в
точках ![]() .
.
4. В интервале ![]()
![]()
![]() функция убывает; в
интервале
функция убывает; в
интервале ![]()
![]()
![]() функция возрастает; в
интервале
функция возрастает; в
интервале ![]()
![]()
![]() функция убывает. Так как
при переходе через критическую точку
функция убывает. Так как
при переходе через критическую точку ![]() производная меняет
знак с минуса на плюс, то это точка минимума. При переходе же через точку
производная меняет
знак с минуса на плюс, то это точка минимума. При переходе же через точку ![]() производная меняет
знак с плюса на минус. Поэтому
производная меняет
знак с плюса на минус. Поэтому ![]() - точка максимума функции.
- точка максимума функции.
5. Вычисляем ![]() ,
, ![]() .
.
Составим
таблицу.
|
|
|
|
|
|
|
|
|
- |
|
+ |
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Второе достаточное условие
существования экстремума дается следующей теоремой.
Если первая производная ![]() дважды
дифференцируемой функции
дважды
дифференцируемой функции ![]() равна нулю в некоторой
точке
равна нулю в некоторой
точке ![]() , а вторая производная в
этой точке
, а вторая производная в
этой точке ![]() положительна
(отрицательна), то
положительна
(отрицательна), то ![]() есть точка минимума
(максимума) функции
есть точка минимума
(максимума) функции ![]() .
.
Смысл теоремы в том, что
знак второй производной позволяет судить о монотонности первой производной, о
смене ее знака при переходе через точку ![]() и, следовательно, о
наличии экстремума.
и, следовательно, о
наличии экстремума.
Заметим, что второе правило исследования функции на
экстремум отличается от первого правила
только пунктом 4, устанавливающим наличие экстремума: здесь следует найти вторую производную ![]() и определить ее знак в
каждой критической точке.
и определить ее знак в
каждой критической точке.
Пример 2. Найдите экстремумы функции ![]() .
.
Решение.
1. Область определения функции ![]() интервал
интервал ![]() .
.
2. ![]() .
.
3. ![]() существует в
существует в ![]() и обращается в нуль в
точке
и обращается в нуль в
точке ![]() .
.
4. Находим
![]() и вычисляем
и вычисляем ![]() . Следовательно, точка
. Следовательно, точка ![]() - точка максимума
функции.
- точка максимума
функции.
5. Вычисляем 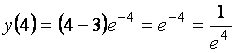 .
.
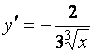 , при
, при