Задача о касательной

Пусть дана некоторая непрерывная функция . Графиком ее будет какая-то кривая .

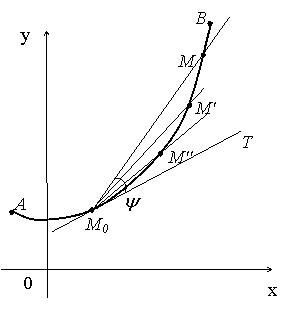Выберем на кривой произвольную точку и, зафиксировав ее, возьмем на этой же кривой произвольным образом еще одну точку

Проведем секущую Станем затем приближать точку к точке по кривой (на чертеже точки , ). Секущая будет при этом поворачиваться.

Может случиться, что при неограниченном приближении точки к по кривой (с любой стороны) секущая будет стремиться к некоторому предельному положению.

Тогда предельное положение секущей и называется касательной к кривой в данной ее точке .

При этом, говоря о предельном положении секущей , мы имеем в виду следующее: существует такая прямая , что угол между нею и секущей (точнее говоря, один из этих углов) стремится к нулю, когда длина хорды стремится к нулю: .

Введя это определение, рассмотрим задачу о проведении касательной к данной кривой . Предположим, что эта кривая имеет в данной точке касательную , образующую с положительным направлением оси угол , отличный от прямого. Задача будет решена, если найдем угловой коэффициент касательной .

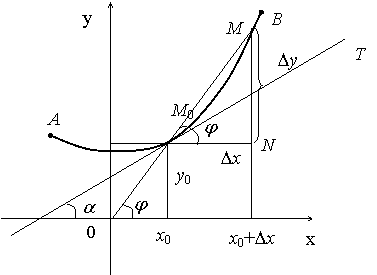
Для решения этой задачи поступим следующим образом: дадим приращение и, вычислив соответствующее приращение функции , возьмем на кривой точку .

Проведем затем секущую . Пусть она образует с положительным направлением оси угол (он может быть как больше, так и меньше угла ). Для угла между секущей и касательной имеем: , откуда по определению касательной , или .

Так как кривая пересекается всякой прямой, параллельной оси , не более чем в одной точке, то для прямой угол отличен от прямого и существует. Проведем на рисунке и из найдем .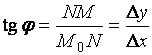

Устремим теперь к нулю. Тогда в силу непрерывности функции и будет стремиться к нулю.

Отсюда , т.е. при и . Но при имеем: и вследствие непрерывности тангенса . Отсюда следует, что существует и предел , который также равен , т.е. существует , так что .

Итак, чтобы найти угловой коэффициент касательной в точке к кривой , где - непрерывная функция, достаточно уметь находить предел вида:

.
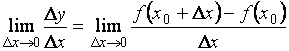