Замкнутые СМО

До сих пор мы рассматривали системы, в которых входящий поток никак не связан с выходящим. Такие системы называются разомкнутыми. В некоторых же случаях обслуженные требования после задержки опять поступают на вход. Такие СМО называются замкнутыми. Поликлиника, обслуживающая данную территорию, бригада рабочих, закрепленная за группой станков, являются примерами замкнутых систем.

В замкнутой СМО циркулирует одно и то же конечное число потенциальных требований. Пока потенциальное требование не реализовалось в качестве требования на обслуживание, считается, что оно находится в блоке задержки. В момент реализации оно поступает в саму систему. Например, рабочие обслуживают группу станков. Каждый станок является потенциальным требованием, превращаясь в реальное в момент своей поломки. Пока станок работает, он находится в блоке задержки, а с момента поломки до момента окончания ремонта - в самой системе. Каждый рабочий является каналом обслуживания.

Пусть n - число каналов обслуживания, s - число потенциальных заявок, n<s, - интенсивность потока заявок каждого потенциального требования, μ -интенсивность обслуживания:

ρ=.

Вероятность простоя системы определяется формулой

Р₀=.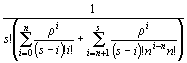

Финальные вероятности состояний системы

P_k= при k<n, P_k= при .

Через эти вероятности выражается среднее число занятых каналов

=P₁+2P₂+…+n(P_n+P_n+1+…+P_s) или

=P₁+2P₂+…+(n-1)P_n-1+n(1-P₀-P₁-…-P_n-1).

Через находим абсолютную пропускную способность системы

A=,

а также среднее число заявок в системе

М=s-=s-.

Пример 1. На вход трехканальной СМО с отказами поступает поток заявок с интенсивностью =4 заявки в минуту, время обслуживания заявки одним каналом t_обсл=1/μ =0,5 мин. Выгодно ли с точки зрения пропускной способности СМО заставить все три канала обслуживать заявки сразу, причем среднее время обслуживания уменьшается втрое? Как это скажется на среднем времени пребывания заявки в СМО?

Решение. Находим вероятность простоя трехканальной СМО по формуле

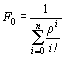
ρ = /μ =4/2=2, n=3,

Р₀=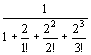==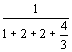0,158.

Вероятность отказа определяем по формуле

Р_отк=Р_n==

P_отк= 0,21.

Относительная пропускная способность системы

Р_обсл=1-Р_отк1-0,21=0,79.

Абсолютная пропускная способность системы

А= Р_обсл3,16.

Среднее число занятых каналов определяем по формуле

1,58, доля каналов, занятых обслуживанием,

q=0,53.

Cреднее время пребывания заявки в СМО находим как вероятность того, что заявка принимается к обслуживанию, умноженную на среднее время обслуживания: t_СМО0,395 мин.

Объединяя все три канала в один, получаем одноканальную систему с параметрами μ =6, ρ =2/3. Для одноканальной системы вероятность простоя

Р₀===0,6,

вероятность отказа

Р_отк=ρ Р₀==0,4,

относительная пропускная способность

Р_обсл=1-Р_отк=0,6,

абсолютная пропускная способность

А= Р_обсл=2,4.

Среднее время пребывания заявки в СМО

t_СМО=Р_обсл==0,1 мин.

В результате объединения каналов в один пропускная способность системы снизилась, так как увеличилась вероятность отказа. Среднее время пребывания заявки в системе уменьшилось.

Пример 2. На вход трехканальной СМО с неограниченной очередью поступает поток заявок с интенсивностью =4 заявки в час, среднее время обслуживания одной заявки t = 1/μ =0,5 ч. Найти показатели эффективности работы системы.

Для рассматриваемой системы n=3, =4, μ =1/0,5=2, ρ = /μ =2, ρ /n=2/3<1. Определяем вероятность простоя по формуле

Р=.

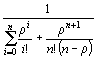P₀=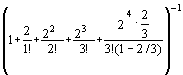=1/9.

Среднее число заявок в очереди находим по формуле

L=.

L==.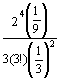

Среднее время ожидания заявки в очереди считаем по формуле

t=.

t==0,22 ч.

Среднее время пребывания заявки в системе

Т=t+0,22+0,5=0,72.

Пример 3. В парикмахерской работают 3 мастера, а в зале ожидания расположены 3 стула. Поток клиентов имеет интенсивность =12 клиентов в час. Среднее время обслуживания t_обсл=20 мин. Определить относительную и абсолютную пропускную способность системы, среднее число занятых кресел, среднюю длину очереди, среднее время, которое клиент проводит в парикмахерской.

Для данной задачи n=3, m=3, =12, μ =3, ρ =4, ρ /n=4/3. Вероятность простоя определяем по формуле

Р₀=.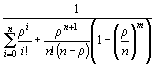

P₀=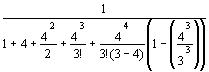0,012.

Вероятность отказа в обслуживании определяем по формуле

Р_отк=Р_n+m = .

P_отк=P_n+m0,307.

Относительная пропускная способность системы, т.е. вероятность обслуживания

P_обсл=1-P_отк1-0,307=0,693.

Абсолютная пропускная способность

А=Р_обсл12.

Среднее число занятых каналов

.

Средняя длина очереди определяется по формуле

L=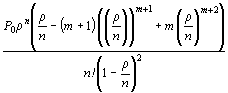

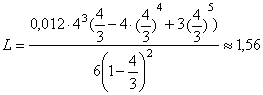
Среднее время ожидания обслуживания в очереди

t= ч.

Среднее число заявок в СМО

M=L+.

Среднее время пребывания заявки в СМО

Т=М/0,36 ч.

Пример 4. Рабочий обслуживает 4 станка. Каждый станок отказывает с интенсивностью =0,5 отказа в час, среднее время ремонта t_рем=1/μ =0,8 ч. Определить пропускную способность системы.

Эта задача рассматривает замкнутую СМО, μ =1,25, ρ =0,5/1,25=0,4. Вероятность простоя рабочего определяем по формуле

Р₀=.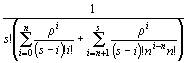

.

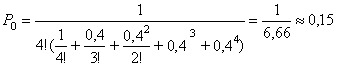Вероятность занятости рабочего Р_зан=1-Р₀. Если рабочий занят, он налаживает μ станков в единицу времени, пропускная способность системы А=(1-P₀)μ=0,85μ станков в час.